Содержание
правила заполнения — Квалифицированная подпись
от Дежурный
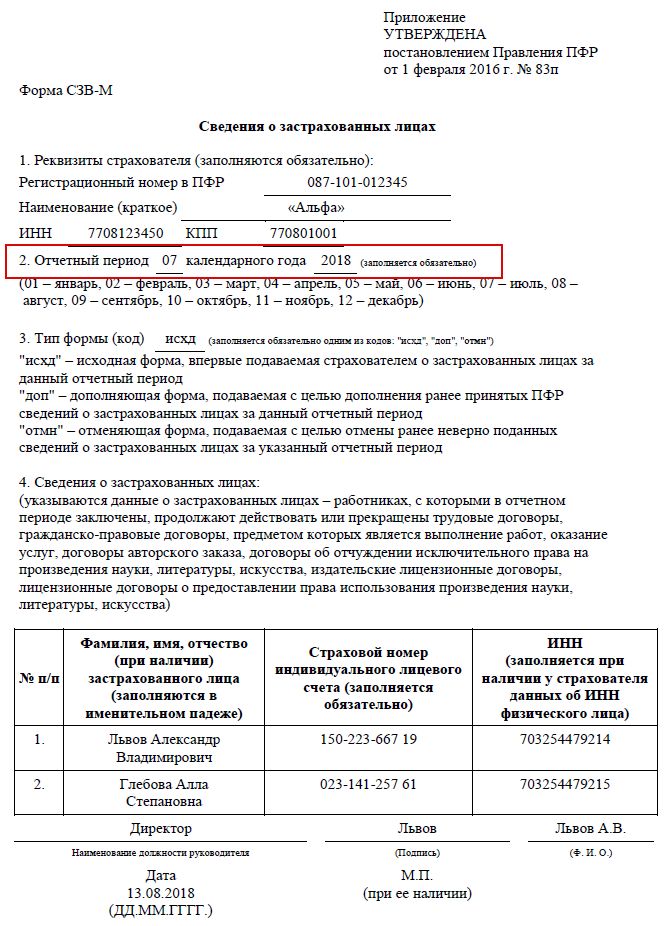
С 1 января 2023 года произойдет объединение Пенсионного фонда РФ и Фонда социального страхования РФ. Как следствие, изменятся формы и состав отчетности, которая будет представляться в объединенный фонд. Рассмотрим, что будет представлять собой новая форма ЕФС-1, которая заменит СЗВ-ТД. СЗВ-СТАЖ. СЗВ-М. 4-ФСС к ДСВ-3.
Изменения 2023 года: Социальный фонд России вместо ПФР и ФСС РФ
С 2023 года вместо Пенсионного фонда РФ и Фонда социального страхования РФ будет действовать единый фонд – Фонд пенсионного и социального страхования Российской Федерации (Федеральный закон от 14.07.2022 № 236-ФЗ «О Фонде пенсионною и социального страхования Российской Федерации»). Кратко фонд будет именоваться Социальный фонд России, а сокращенно – СФР.
Соответственно, с нового года станут неактуальными действующие сейчас формы. СЗВ-ТД. СЗВ-СТАЖ. СЗВ-М, 4-ФСС, ДСВ-3. Вместо данных форм будет введена единая форма сведений (п. 2 ст. 8 Федерального закона от 01.04.1996 № 27-ФЗ «Об индивидуальном (персонифицированном) учете в системах обязательного пенсионного страхования и обязательного социального страхования» в редакции, действующей с 01.03.2022). В единую форму войдет также информация о страховых взносах на обязательное социальное страхование (несчастные случай и профзаболевания), поэтому отпадает необходимость в отдельной форме 4-ФСС.
СЗВ-ТД. СЗВ-СТАЖ. СЗВ-М, 4-ФСС, ДСВ-3. Вместо данных форм будет введена единая форма сведений (п. 2 ст. 8 Федерального закона от 01.04.1996 № 27-ФЗ «Об индивидуальном (персонифицированном) учете в системах обязательного пенсионного страхования и обязательного социального страхования» в редакции, действующей с 01.03.2022). В единую форму войдет также информация о страховых взносах на обязательное социальное страхование (несчастные случай и профзаболевания), поэтому отпадает необходимость в отдельной форме 4-ФСС.
Новая форма ЕФС-1
На данный момент единая форма еще не утверждена, но Правление ПФР подготовило проект Постановления об утверждении единой формы и правилах ее заполнения. С максимальной долей вероятности, с 2023 года будет использоваться единая форма, предложенная данным проектом. Поэтому заранее ознакомимся с особенностями данного документа.
Итак, форма будет иметь краткое наименование ЕФС-1. Состоять она будет из титульного листа и двух разделов:
Раздел 1 – «Сведения о трудовой (иной) деятельности, страховом стаже, заработной плате и дополнительных страховых взносах на накопительную пенсию»;
Раздел 2 – «Сведения о начисленных страховых взносах на обязательное социальное страхование от несчастных случаев на производстве и профессиональных заболеваний».
Каждый раздел содержит еще несколько подразделов, которые имеют свои особенности заполнения и сроки представления. Нет необходимости всегда представлять полностью заполненную форму. Организация может представлять конкретные разделы и подразделы в соответствии с установленными сроками их представления (п. 1.11 Проекта, но титульный лист надо заполнять всегда, независимо от комплектации отчета).
Заполнение раздела 1
Раздел 1 фактически заменяет формы СЗВ-ТД, СЗВ-СТАЖ и ДСВ-3. Обратите внимание: в данный раздел надо будет включать информацию не только о работниках, но и об исполнителях по гражданско-правовым договорам.
Раздел 1 состоит из подразделов:
– подраздел 1 «Сведения о трудовой (иной) деятельности, страховом стаже, заработной плате зарегистрированного лица (ЗЛ)».
Этот подраздел содержит общие сведения о работнике (исполнителе по договору ГПХ). Поэтому заполнять этот подраздел надо обязательно, если вы заполняете один из следующих подразделов раздела 1.
– подраздел 1.1. «Сведения о трудовой (иной) деятельности»
Этот подраздел содержит информацию, которая сейчас отражается в СЗВ-ТД. Но еще раз отметим, что заполнять данный раздел надо будет не только, когда будут иметь место кадровые мероприятия в отношении работников, но и в отношении исполнителей по договорам ГПХ, поэтому появляются свои нюансы.
Вводятся новые коды «НАЧАЛО ДОГОВОРА ГПХ», «ОКОНЧАНИЕ ДОГОВОРА ГПХ». Отметим, что проект ЕФС-1 создавался до введения изменений в трудовое законодательство относительно необходимости приостановления трудовых договоров с мобилизованными работниками. Поэтому, очевидно, что Проект будет дополнен кодами «ПРИОСТАНОВЛЕНИЕ» и «ВОЗОБНОВЛЕНИЕ».
Представлять сведения из подраздела 1.1. надо будет по правилам, действующим сейчас в отношении формы СЗВ-ТД: при приеме/увольнении, заключении/расторжении договора ГПХ – не позднее следующего рабочего дня; при переводе, переходе на электронную трудовую книжку и пр. – не позднее 25-го числа следующего месяца.
– подраздел 1.2. «Сведения о страховом стаже»
Данный подраздел заменит форму СЗВ-СТАЖ. Состав информации во многом схож с действующей формой, но имеются нюансы. Например, вводится графа «Занятость» в разделе «Условия досрочного назначения страховой пенсии», а также информация о результатах СОУТ. Сдавать подраздел надо не позднее 25 января следующего года.
– подраздел 1.3 – актуален только для работников государственных и муниципальных учреждений.
– подраздел 2 – заполняется в случае, если работники имеют право на досрочную пенсию. Сдавать подраздел надо не позднее 25 января следующего года.
– подраздел 3 – «Сведения о застрахованных лицах, за которых перечислены дополнительные страховые взносы на накопительную пенсию и уплачены взноси работодателя». Повторяет сведения, которые сейчас отражаются в ДСВ-3.
Сдавать подраздел надо ежеквартально, не позднее 25-го числа месяца, следующего за отчетным кварталом.
Заполнение раздела 2
Раздел 2 формы ЕФС-1 в принципе повторяет действующую сейчас форму 4-ФСС. Сдавать раздел надо ежеквартально, не позднее 25 числа месяца, следующего за отчетным кварталом.
Сдавать раздел надо ежеквартально, не позднее 25 числа месяца, следующего за отчетным кварталом.
Математика SVM | Math Behind Support Vector Machine
Эта статья была опубликована в рамках блога по науке о данных.
Введение
Одним из классификаторов, с которыми мы сталкиваемся при изучении машинного обучения, является машина опорных векторов или SVM. Этот алгоритм является одним из самых популярных алгоритмов классификации, используемых в машинном обучении.
В этой статье мы узнаем о математике, лежащей в основе машины опорных векторов для задачи классификации, о том, как она классифицирует классы и дает прогноз.
Содержание
- Нежное введение в метод опорных векторов (SVM)
- Несколько понятий, которые нужно знать, прежде чем узнать секрет алгоритма
- Погружение глубоко в море математики
- 3.1 Где использовать SVM / Предыстория SVM
- 3.1.1 Случай 1: Идеально разделенный двоичный классифицированный набор данных
- 3.
 1.2 Уравнение идеального разделения
1.2 Уравнение идеального разделения
- 3.2 Случай 2: набор данных несовершенного разделения
- 3.2.1 Окончательное уравнение для решения несовершенного разделения
- 3.2.2 Первичный – Двойственный – Лагранжев
- 3.2.3 Использование ядра для получения окончательных результатов
- 3.1 Где использовать SVM / Предыстория SVM
- Конечные точки
1. Машина опорных векторов
A Машина опорных векторов или SVM — это алгоритм машинного обучения, который просматривает данные и сортирует их по одной из двух категорий.
Машина опорных векторов — это линейный алгоритм машинного обучения с учителем, который чаще всего используется для решения задач классификации и также называется классификацией опорных векторов.
Существует также подмножество SVM, называемое SVR, что означает регрессию опорных векторов, в которой используются те же принципы для решения задач регрессии.
SVM наиболее часто используется и эффективен из-за использования метода ядра, который в основном помогает решить нелинейность уравнения очень простым способом.
П.С. — Так как эта статья написана с упором на математическую часть. Пожалуйста, обратитесь к этой статье для полного обзора работы алгоритма
2. Основные темы для SVM
Машина опорных векторов в основном помогает сортировать данные по двум или более категориям с помощью границы для различения похожих категорий.
Итак, сначала давайте пересмотрим формулы того, как данные представлены в пространстве, и что такое уравнение линии, которое поможет разделить похожие категории, и, наконец, формулу расстояния между точкой данных и линией (граница, разделяющая категории).
2.1 Точка в пространстве
Предположим, у нас есть некоторые данные, в которых нас (алгоритм SVM) просят различать мужчин и женщин на основе сначала изучения характеристик обоих полов, а затем точного обозначения невидимых данных, если кто-то мужчина или женщина.
В этом примере характеристики, которые помогут различать пол, в основном называются признаками в машинном обучении.
Домен
, совместный домен, диапазон
Предполагая, что мы уже знакомы с понятием домена, диапазона и совместного домена при определении функции в реальном пространстве. (Если нет, пожалуйста, нажмите на изображение для понимания концепции с примером)
Когда мы определяем x в реальном пространстве, мы понимаем его домен, а при отображении функции для y = f(x) мы получаем диапазон и со-область.
Итак, изначально нам даны данные, которые должны быть разделены алгоритмом. 9D здесь — векторное пространство с размерностью D, для этого алгоритма не обязательно иметь представление об этом понятии.
Мы применяем аналогичную концепцию домена, диапазона, отображения функции для точек данных здесь, вместо реального пространства у нас есть векторное пространство для x.
Далее, отображая точку на сложном пространстве признаков x,
Φ(x) ∊ R M
Преобразованное пространство признаков для каждого входного признака, сопоставленного с преобразованным базисным вектором Φ(x), можно определить как :
2. 2 Граница принятия решения
2 Граница принятия решения
Итак, теперь, когда мы представили наши точки визуально, наша следующая задача состоит в том, чтобы разделить эти точки с помощью линии, и именно здесь появляется термин граница решения.
Граница принятия решения является основным разделителем для разделения точек на соответствующие классы.
(Как и почему я говорю, что основной разделитель, а не просто любой разделитель, мы рассмотрим, понимая математику)
Уравнение гиперплоскости :
Уравнение главной разделительной линии называется уравнением гиперплоскости.
Давайте посмотрим на уравнение прямой с наклоном m и точкой пересечения c.
Уравнение принимает вид: mx + c = 0
(Обратите внимание: мы поместили прямую/линейную линию, которая является 1-мерной, в 2-мерном пространстве)
Уравнение гиперплоскости, разделяющее точки (для классификации), теперь может быть легко записано как:
H: w T (x) + b = 0
Здесь: b = член пересечения и смещения уравнения гиперплоскости
В D-мерном пространстве гиперплоскость всегда будет оператором D-1.
Например, для двумерного пространства гиперплоскость — это прямая линия (одномерная).
2.3 Измеритель расстояния
Теперь, когда мы увидели, как представлять точки данных и как провести разделительную линию между точками. Но при подгонке разделительной линии мы, очевидно, хотели бы такую линию, которая могла бы наилучшим образом разделить точки данных с наименьшим количеством ошибок/ошибок промаха классификации.
Таким образом, чтобы иметь наименьшие ошибки в классификации точек данных, эта концепция потребует от нас сначала узнать расстояние между точкой данных и разделительной линией.
Расстояние любой линии, ax + by + c = 0 от заданной точки, скажем, (x 0 , y 0 ) определяется как d.
Точно так же расстояние уравнения гиперплоскости: w T Φ(x) + b = 0 от заданного точечного вектора Φ(x 0 ) можно легко записать как:
здесь ||w||2 — евклидова норма длины w, определяемая как:
[stextbox id=’alert’ shadow=”false”] Теперь, когда термины ясны, давайте углубимся в используемый алгоритм. [/stextbox]
[/stextbox]
3. Рыбы много
Математика в море
3.1 Фон
Мы говорили о примере дифференциации полов, поэтому такие задачи называются задачами классификации. Теперь проблема классификации может иметь только два (двоичных) класса для разделения или может иметь более двух, что известно как проблемы классификации с несколькими классами.
Но не все прогностические модели классификации поддерживают многоклассовую классификацию, такие алгоритмы, как логистическая регрессия и машины опорных векторов (SVM), были разработаны для двоичной классификации и изначально не поддерживают задачи классификации с более чем двумя классами.
Но если кто-то все еще хочет использовать алгоритмы бинарной классификации для задач множественной классификации, один из широко используемых подходов состоит в том, чтобы разбить наборы данных мультиклассовой классификации на несколько наборов данных бинарной классификации, а затем подобрать модель бинарной классификации для каждого из них.
Двумя различными примерами этого подхода являются стратегии «Один против остальных» и «Один против одного». О двух подходах можно прочитать здесь.
Двигаясь вперед к основной теме понимания математики, мы рассмотрим проблему классификации двоичных классов по двум причинам:
- Как уже упоминалось выше, SVM работает намного лучше для бинарного класса
- Было бы легко понять математику, поскольку наша целевая переменная (переменная / невидимые данные, предназначенные для прогнозирования, является ли точка мужчиной или женщиной)
- Примечание. Это будет подход «один против одного».
3.1.1 Случай 1: (Идеальное разделение для двоичных классифицированных данных) –
Продолжая наш пример, если гиперплоскость сможет точно различать самцов и самок без какой-либо ошибочной классификации, тогда этот случай разделения известен как идеальное разделение.
Здесь, на рисунке, если самцы зеленые, а самки красные, и мы можем видеть, что гиперплоскость, которая здесь является линией, прекрасно различает два класса.
Обобщая, данные имеют две классификации , положительную и отрицательную группу , и полностью разделимы, что означает, что гиперплоскость может точно разделить *тренировочные классы*.
**
( Обучающие данные — Данные, с помощью которых алгоритм/модель изучает шаблон того, как различать, просматривая признаки данные, где даны только признаки, и теперь модель скажет самец это или самка)
**
Теперь может быть много гиперплоскостей, дающих 100% точность, , как видно на фотографии.
«» Итак, чтобы выбрать оптимальную/наилучшую гиперплоскость, поместите гиперплоскость прямо в центр, где максимальное расстояние от ближайших точек и далее дайте наименьшие ошибки теста. “”
Обратите внимание: мы должны стремиться к наименьшему количеству ошибок ТЕСТА, а НЕ к ошибкам ОБУЧЕНИЯ.
Итак, мы должны максимизировать расстояние, чтобы дать некоторое пространство уравнению гиперплоскости, которое также является целью/основной идеей SVM.
Цель алгоритма SVM:
Итак, теперь нам нужно:
Нахождение гиперплоскости с максимальным запасом (зазор — это в основном защищенное пространство вокруг уравнения гиперплоскости), и алгоритм пытается получить максимальный запас с ближайшими точками (известными как опорные векторы).
Другими словами, “ Цель состоит в том, чтобы максимизировать минимальное расстояние. ” для расстояния (упомянутого ранее в разделе 2)
, дано:
Итак, цель понятна. Делая прогнозы на обучающих данных, которые были бинарно классифицированы как положительные и отрицательные группы, если точка заменена положительной группой в уравнении гиперплоскости, мы получим значение больше 0 (ноль). Математически,
w T ( Φ(x)) + b > 0
И предсказания из отрицательной группы в уравнении гиперплоскости дадут отрицательное значение как
w T ( Φ(x)) + b < 0.
Но здесь знаки были об обучающих данных, именно так мы обучаем нашу модель. Что для положительного класса дайте положительный знак, а для отрицательного — отрицательный.
Но при тестировании этой модели на тестовых данных, если мы правильно предсказываем положительный класс (положительный знак или знак больше нуля) как положительный, то два положительных результата дают положительный и, следовательно, результат больше нуля. То же самое применимо, если мы правильно предсказываем отрицательную группу, поскольку два отрицательных значения снова дадут положительный результат.
Но если ошибка модели классифицирует положительную группу как отрицательную группу, тогда один плюс и один минус составляют минус, следовательно, в целом меньше нуля.
Подводя итог вышеизложенному:
Произведение предсказанной и фактической метки будет больше 0 (нуля) при правильном предсказании, в противном случае меньше нуля.
Для идеально разделимых наборов данных оптимальная гиперплоскость правильно классифицирует все точки, дополнительно заменяя оптимальные значения в весовом уравнении.
Здесь :
arg max — это аббревиатура для аргументов максимумов, которые в основном являются точками области определения функции, в которых значения функции максимальны.
(Для дальнейшей работы с arg max в машинном обучении читайте здесь.)
Далее, выведение независимого члена веса наружу дает:
Внутренний член (мин n y n |w T Φ(x) + b | ) в основном представляет минимальное расстояние точки до границы решения и ближайшую точку к границе решения H.
Изменение масштаба расстояния до ближайшей точки как 1 т.е. (min n y n |w T Φ(x) + b |) = 1. Здесь векторы остаются в одном направлении и уравнение гиперплоскости не изменится. Это похоже на изменение масштаба изображения; объекты расширяются или сжимаются, но направления остаются прежними, и изображение остается неизменным.
Изменение масштаба расстояния осуществляется путем подстановки,
Уравнение теперь становится (описывая, что каждая точка находится на расстоянии не менее 1/||w||2 от гиперплоскости) как
Эта задача на максимизацию эквивалентна следующей задаче на минимизацию, которая умножается на константу, поскольку они не влияют на результаты.
3.1.2 Первичная форма SVM (идеальное разделение):
Приведенная выше задача оптимизации является первичной формулировкой, поскольку в постановке задачи используются исходные переменные.
3.2 СЛУЧАЙ 2: (не идеальное разделение)
Но все мы знаем, что не бывает ситуации, когда все идеально, а что-то всегда идет наоборот.
В нашем примере гендерной классификации мы не можем ожидать, что модель даст такое уравнение гиперплоскости, которое идеально разделит оба пола, всегда будет одна или несколько точек, которые не попадут в свою категорию, в то время как оптимальная гиперплоскость уравнение подходит, известное как классификация промахов. (Как показано на изображении ниже)
(Как показано на изображении ниже)
Таким образом, мы не можем ожидать идеального/идеального корпуса. Здесь мы становимся умнее модели и позволяем модели сделать несколько ошибок при классификации точек и, следовательно,
И, следовательно, добавьте резервную переменную в качестве штрафа за каждую ошибку классификации для каждой точки данных, представленной β (бета). Таким образом, отсутствие штрафа означает, что точка данных правильно классифицирована, β = 0, и при любой классификации промахов β > 1 в качестве штрафа.
3.2.1 Первичная форма SVM (неидеальное разделение):
Здесь: для β и C
Slack для каждой переменной должен быть как можно меньше и дополнительно регулироваться гиперпараметром C
Приведенное выше уравнение является примером выпукло-квадратичной оптимизации , поскольку целевая функция квадратична по W, а ограничения линейны по W и β.
Раствор для первичной формы : (не идеальное разделение):
Так как у нас есть Φ, который имеет комплексное обозначение. мы бы переписали уравнение.
Концепция
в основном состоит в том, чтобы избавиться от Φ и, следовательно, переписать основную формулировку в двойной формулировке, известной как двойная форма проблемы, и решить полученную задачу оптимизации ограничений с помощью метода множителей Лагранжа.
Другими словами:
Двойная форма: переписывает ту же задачу, используя другой набор переменных. Таким образом, альтернативная формулировка поможет устранить зависимость от Φ, а уменьшение эффекта будет выполнено с помощью Kernelization.
Метод множителя Лагранжа: Это стратегия поиска локальных минимумов или максимумов функции при условии, что одно или несколько уравнений должны точно удовлетворяться выбранными значениями переменных.
Кроме того, формальное определение двойственной задачи может быть определено как:
Двойственная лагранжева задача получается путем формирования сначала лагранжиана уже полученной задачи минимизации с помощью множителя Лагранжа, чтобы к целевой функции можно было добавить новые ограничения , а затем будет решаться для значений первичной переменной , которые минимизируют исходную целевую функцию
.
Это новое решение делает основные переменные функциями множителей Лагранжа и называется двойственными переменными, поэтому новая задача состоит в том, чтобы максимизировать целевую функцию для двойственных переменных с новыми производными ограничениями.
В этом блоге очень хорошо объясняется работа множителей Лагранжа.
Возьмем пример применения множителя Лагранжа для лучшего понимания того, как преобразовать основную формулу с использованием множителей Лагранжа для решения задачи оптимизации .
Ниже x представлена исходная основная переменная и минимизация функции f при наборе ограничений, заданном g, и переписывание для нового набора переменных, называемых множителями Лагранжа.
Решение простых переменных путем дифференцирования Лагранжа без ограничений.
И, наконец, обратная подстановка в уравнение Лагранжа и переписывание ограничений
Возвращаясь к нашей первичной форме:
Шаг 1: Получение прямого числа и определение лагранжевой формы из простого числа
Шаг 2: Получение решения путем представления простого числа в форме двойственного числа
Шаг 3: Подставить полученные значения в лагранжеву форму
Окончательная двойная форма из приведенного выше упрощения:
Вышеупомянутая двойная форма все еще имеет Φ членов, и здесь это легко решается с помощью Kernelization
Ядро по определению избегает явного отображения, необходимого для получения алгоритмов линейного обучения для изучения нелинейной функции или границы решения. Для всех x и x’ во входном пространстве Φ могут быть выражены определенные функции k(x,x’) как скалярный продукт в другом пространстве Ψ. Функция
Для всех x и x’ во входном пространстве Φ могут быть выражены определенные функции k(x,x’) как скалярный продукт в другом пространстве Ψ. Функция
упоминается как Ядро . Короче говоря, для машинного обучения ядро определяется как записанное в виде «карты функций»
который удовлетворяет
Для лучшего понимания ядер можно обратиться к этой ссылке квора
Ядро имеет два свойства:
Он симметричен по своей природе k(x n , x m ) = k(x m , x n )
Положительный полуопределенный
Чтобы иметь представление о работе ядер, может быть полезна эта ссылка квора.
По определению ядра мы можем подставить эти значения
Итак, подставив свойства ядра и по определению ядра в нашу двойственную форму,
Мы получаем Новое уравнение как:
И это решение не содержит Φ, и его гораздо проще вычислить.
-й это была математика, стоящая за моделью SVM.
4. Указывая на все шаги, упомянутые выше.
Наконец-то мы подошли к концу статьи, и подводя итог, весь бред написанный выше
- Всякий раз, когда нам дается какой-либо тестовый вектор признаков x для предсказания, отображается в комплекс Φ(x) и просят предсказать, что в основном является w T Φ(x)
- Затем перепишите его, используя двойственные значения, чтобы предсказание полностью не зависело от базиса сложных признаков Φ
- И далее предсказывается с использованием ядер
- Отсюда делаем вывод, что нам не нужен сложный базис, чтобы хорошо моделировать неразделимые данные, и ядро делает свою работу.
Надеюсь, мне удалось раскрыть основы интуиции и математики, лежащие в основе SVM, для модели классификатора и помня о длине статьи, я попытался прикрепить все важные ссылки к соответствующим ссылкам внутри статьи.Это было мое понимание задействованной математики в SVM, и я открыт для предложений относительно моей работы здесь
Метод опорных векторов, двойная формулировка, квадратичное программирование и последовательная минимальная оптимизация | by Suraj Donthi
Это математически ориентированный подход к интуиции, лежащей в основе SVM, и алгоритмов оптимизации, используемых для ее решения. Эта статья служит универсальным руководством по демистификации внутренней работы SVM.
Машина опорных векторов (или первоначально автор — Владимир Вапник называл Сети опорных векторов) использует совершенно иной подход к решению статистических задач (в конкретной Классификации). Этот алгоритм активно использовался в нескольких задачах классификации, таких как классификация изображений, классификатор Bag-of-Words, OCR, прогнозирование рака и многие другие. SVM в основном представляет собой бинарный классификатор, хотя его можно модифицировать для многоклассовой классификации, а также для регрессии. В отличие от логистической регрессии и других моделей нейронных сетей, SVM пытаются максимизировать разделение между двумя классами точек. Блестящая идея использована автором.
В отличие от логистической регрессии и других моделей нейронных сетей, SVM пытаются максимизировать разделение между двумя классами точек. Блестящая идея использована автором.
Ниже приведены концепции , которые мы рассмотрим в этой статье , которые шаг за шагом демистифицируют SVM, а затем улучшают алгоритм, устраняя его недостатки.
- Ванильный (обычный) SVM и его целевая функция
- Мягкая маржа SVM
- Уловка ядра
- Приложение 1. Вывод уравнения максимальной маржи. & Целевая функция
- Приложение 2. Поиск оптимума Целевой фн. с использованием лагранжиана, двойной формулировки и квадратичного программирования
∘ Общий метод решения для минимума
∘ Решение для минимума, когда присутствуют ограничения
∘ Kuhn — Условия Tucker
∘ Двойственность и дополнительная слабая - Приложение 3 — вывод оптимальной для софт -края
- Заключение
- 70017. просто возьмите формальное определение SVM из Википедии:
Машина опорных векторов строит гиперплоскость или набор гиперплоскостей в многомерном или бесконечномерном пространстве, которые можно использовать для классификации, регрессии или других задач, таких как обнаружение выбросов.
 .
.Подождите, но слишком много технических терминов! Давайте просто упростим его и сохраним только необходимую информацию!
Во-первых, SVM создает гиперплоскость ( простая линия в n измерениях ). Как и в приведенном ниже GIF, эта гиперплоскость должна наилучшим образом разделить два класса пополам. Это все, что делают SVM… Остальное — начинка! ( бесконечномерное пространство, регрессия, обнаружение выбросов и т. д. )
Теперь построим ОПТИМАЛЬНАЯ ГИПЕРПЛОСКОСТЬ она опирается на две другие гиперплоскости, которые параллельны и равноудалены от нее с обеих сторон!
Эти две опорные гиперплоскости лежат в самых крайних точках между классами и называются опорными векторами .
Следовательно, нам просто нужно найти опорные гиперплоскости ( используя для простоты ), которые имеют максимальное расстояние между собой! Отсюда мы можем легко получить ОПТИМАЛЬНЫЙ ГИПЕРПЛАН .
 Это называется просто Гиперплоскость максимальной маржи . Расстояние между опорными гиперплоскостями называется Margin .
Это называется просто Гиперплоскость максимальной маржи . Расстояние между опорными гиперплоскостями называется Margin .Источник: изображение автора
Следовательно, наша цель — просто найти максимальный запас M. Используя векторные операции, мы можем найти это (учитывая ОПТИМАЛЬНУЮ ГИПЕРПЛОСКОСТЬ ( w.x+b=0 ) ), маржа равна:
Следовательно, максимальная маржа M :
Для удобства математики целевая функция принимает вид (подробное объяснение в Приложении 1):
Обратите внимание, что наша цель сводилась к нахождению оптимального w из уравнения w.x+b= 0 !
Однако это также связано с ограничением, заключающимся в том, что точки в классе не должны лежать в пределах двух опорных гиперплоскостей! Математически это можно представить как:
Так что же означают эти ограничения?
Это означает, что внутри гиперплоскости не может быть точек, как показано на рисунке ниже, и это называется Hard Margin SVM (Vanilla SVM).

Источник: изображение автора
Это большой недостаток SVM! Два класса должны быть полностью разделимы. Этого никогда не бывает в реальных наборах данных! Вот где Soft Margin SVM вступают в игру🎉😃!
Прежде чем двигаться дальше, всего один вопрос! Используют ли SVM градиентный спуск для поиска минимумов ? Ни за что! (большинство людей этого не знают). Минимумы находятся непосредственно путем решения производных Objective функции . Поскольку существуют ограничения, нам нужно сначала взять лангранжиан целевой функции , чтобы найти минимумы. Вы можете найти полный вывод в Приложении 2 (рекомендую вам прочитать его!).
Как упоминалось выше, SVM Soft Margin могут обрабатывать классы с неотделимыми точками данных. Рисунок ниже ясно объясняет то же самое!
Итак, вот суть идеи Soft Margin:
Чтобы позволить SVM делать некоторые ошибки и при этом сохранить как можно большее поле.

Источник: изображение автора
Теперь, как он может это сделать, но не ванильные SVM? Этот фактор представляет собой расстояние, которое точка данных превышает от соответствующей опорной гиперплоскости до другого класса.
Следовательно, если точка данных находится в пределах границы (опорной гиперплоскости), штрафной коэффициент 𝜉 ᵢ равно 0. В противном случае, если точка данных находится на другой стороне, этот коэффициент 𝜉 ᵢ равен его расстоянию между точкой данных и опорной гиперплоскостью. Следовательно, значение 𝜉 ᵢ является неотрицательным числом.
Это можно резюмировать следующим уравнением:
И в идеале оно должно представлять количество « ошибок », которые делает SVM. Таким образом, наша новая целевая функция будет:
Здесь для малой степени 𝜎 функция F становится количеством ошибок! (Суммирование используется для учета 𝜉 ᵢ всех точек в наборе данных)
Как и для SVM, минимумы могут быть найдены непосредственно путем решения ее производных (лагранжиана производных).

Теперь, оглядываясь назад на то, что мы получили, становится ясно, что мы используем только w.x+b . Это просто линейное уравнение. Это означает, что SVM работает лучше всего, когда вы можете классифицировать данные линейно!
Нелинейные данные. Источник: изображение автора
Это еще одно действительно огромное ограничение! Однако авторы нашли для этого лайфхак💃!! и это трюк с ядром. Проще говоря:
Ядро просто преобразует нелинейные точки данных в линейные точки данных, так что SVM может разделить два класса пополам.
То же самое показано на рисунке ниже.
Преобразование из n-измерения в N-измерение. Источник: Wikimedia
Следовательно, новое уравнение линии будет
Здесь используется хитрый трюк для преобразования точек n-измерения в N-измерение , где N>n .
Ядро 𝜑 должно соответствовать следующим условиям:
Источник: изображение автора
Для SVM используется несколько функций ядра.
 Вот некоторые из популярных:
Вот некоторые из популярных:- Базисная функция Гаусса (RBF) :
, где 𝛾 > 0 .
Особый случай: 𝛾 = 1/2𝜎²
- Gaussian Kernel :
- Polynomial Kernel :
- Sigmoid kernel :
For deriving the Objective function, we assume that the dataset is linearly separable.
Мы знаем, что две опорные гиперплоскости лежат на опорных векторах и между ними нет точек. Следовательно, мы можем сначала рассмотреть срединную гиперплоскость между этими двумя опорными гиперплоскостями:
И учитывая, что расстояние между этой и опорной гиперплоскостями равно 1, мы получаем
Поскольку нет точек, превышающих эти две гиперплоскости, мы можем сделать вывод, что:
Для всех значений с меткой yᵢ=+1 ,
& для всех значений с меткой yᵢ=-1 ,
Мы можем комбинировать два, как показано ниже:
Следовательно, это ограничение для нашей целевой функции (см.
 то же самое в начале статья).
то же самое в начале статья).Теперь, чтобы найти максимальную маржу, ее нужно представить в виде гиперплоскостей. Итак, давайте выведем связь между Margin M и гиперплоскостями.
Источник: Изображение от автора
На приведенном выше рисунке, пусть векторы X₀ и Z ₀ Be Parallel Vector на строках W.x+B = -1 & w.x+b=1 соответственно. Затем
где вектор k является линией, перпендикулярной вектору x₀ и z ₀ .
величина вектора K — M.
Следовательно,
Сейчас с Z ₀ и X₀ Lie On W. x x x x x x₀ Lie на W.
 x x x x x₀ . 1 и w.x+b=-1 ,
x x x x x₀ . 1 и w.x+b=-1 ,Из приведенного выше уравнения. заменив z ₀ ,
Теперь, когда у нас есть, нам нужно максимизировать его,
Следовательно, новая цель, т.е. Целевая функция:
и ограничение неравенства:
Общий метод решения для минимумов
Чтобы найти оптимумы для кривой, мы можем просто
- Взять производную первого порядка,
- Приравнять производную к 0 (для максимумов или минимумов), чтобы получить дифференциальное уравнение.
- Решите дифференциальное уравнение, чтобы найти оптимальные точки.
- Производная 2-го порядка может указать направление, и, следовательно, мы можем сделать вывод, является ли оптимум минимумом или максимумом.
Нахождение минимумов при наличии ограничений
Если в дифференциальном уравнении есть некоторые ограничения, подобные тому, что мы имеем в нашей целевой функции, нам сначала нужно применить множители Лагранжа (что, честно говоря, довольно прямолинейно) !
Если вы наблюдаете приведенное выше уравнение (5), это просто Целевая функция, вычтенная ограничением неравенства! Он должен удовлетворять только критериям αᵢ > 0 , когда ограничение является ограничением равенства.
 Однако приведенные выше уравнения представляют собой уравнений ограничения неравенства . Таким образом, дополнительный набор условий, называемый условиями Куна — Таккера, также должен удовлетворяться. Мы пройдемся по условиям позже.
Однако приведенные выше уравнения представляют собой уравнений ограничения неравенства . Таким образом, дополнительный набор условий, называемый условиями Куна — Таккера, также должен удовлетворяться. Мы пройдемся по условиям позже.Для нахождения оптимумов, как и прежде, возьмем производную первого порядка и приравняем ее к 0:
Чтобы найти оптимальные значения, мы можем просто подставить значения обратно в (5),
Расширяя уравнение. (5) мы получаем,
Теперь подставляя значения в (6) и (7) выше,
Мы можем повторно подставить значение w в уравнение. (6) к приведенному выше уравнению,
Здесь W называется Целевой функционал и является функцией всех ( αᵢ … to … αₙ
4)0049
представлен как Λ (заглавная лямбда).
Этот вывод был необходим для учета ограничения неравенства [уравнение.
 (4)]. Поскольку теперь это учтено, целевой функционал W является новой функцией, которую необходимо оптимизировать вместо уравнения. (3). Это называется ДВОЙНОЙ ФОРМУЛИРОВКОЙ , потому что исходная Целевая функция была изменена!
(4)]. Поскольку теперь это учтено, целевой функционал W является новой функцией, которую необходимо оптимизировать вместо уравнения. (3). Это называется ДВОЙНОЙ ФОРМУЛИРОВКОЙ , потому что исходная Целевая функция была изменена!В то время как экв. (3) был свернут, W должен быть максимизирован.
Поскольку W является квадратным уравнением, это задача квадратичного программирования (QP), и ее можно решить с помощью алгоритма, называемого Sequential Minimal Optimization (SMO) . Если вы когда-либо использовали пакет LibSVM, который является базой для SVM в Scikit-Learn и большинстве других библиотек SVM, вы обнаружите, что пакет LibSVM реализует алгоритм SMO для расчета максимальной маржи !
Наконец, переходим к условиям, которым должны удовлетворять ограничения неравенства.
Kuhn — Условия Tucker
- Двойная осуществимость :
2.
 Бесплатная осуществимость :
Бесплатная осуществимость :3. Стационарные условия :
4. Primal Feasuble (Наше оригинал):
4. Primal Feasuble (Наше оригинал):
40005 4. Primal Feasuble (наш & Complementary Slackness
Когда проблема может быть преобразована в другую задачу, решение которой легче вычислить, а также обеспечивает решение исходной задачи, говорят, что две проблемы демонстрируют Двойственность и наоборот.
Однако все двойные функции не обязательно должны иметь решение, обеспечивающее оптимальное значение для другой. Это можно сделать из приведенного ниже Рис. 1 , где существует Разрыв Двойственности между первичной и двойной проблемой. В Рис. 2 двойственные задачи демонстрируют сильную двойственность и, как говорят, имеют дополнительную нежесткость . Кроме того, из приведенного ниже графика видно, что задача минимизации преобразуется в задачу максимизации.
 Следовательно, нам нужно максимизировать W против αᵢ .
Следовательно, нам нужно максимизировать W против αᵢ .Источник: изображение автора
Как описано ранее, целевая функция для SVM Soft Margin:
Здесь функция F — монотонная выпуклая функция, а C — константа регуляризации.
Следовательно, лагранжиан приведенной выше Целевой функции равен
Используя ту же методологию, что и в методе Hard Margin SVM, мы получаем Целевой функционал as,
Если вы заметили, то дополнительный член здесь равен,
Где,
И ограничения для Целевого функционала:
Следовательно, решая Целевой функционал, мы можем получить оптимальную максимальную маржу.
Из приведенных выше разделов мы можем сделать вывод, что
- Базовые SVM или SVM с жесткой маржой представляют собой бинарные и линейные классификаторы, которые работают только с разделяемыми данными.

- SVM Soft Margin могут работать с неразделимыми данными.
- Ядра можно использовать для преобразования нелинейных данных в линейные данные, к которым можно применить SVM для двоичной классификации.
- Для выполнения многоклассовой классификации можно использовать комбинацию SVM.
- Машины опорных векторов — это чрезвычайно быстрые алгоритмы, поскольку они напрямую определяют максимальную маржу и не используют итеративный процесс, такой как градиентный спуск, для поиска минимумов.
- Бумага о сетях опорных векторов.
- https://www.svm-tutorial.com/2014/11/svm-understanding-math-part-1/
- https://www.svm-tutorial.com/2014/11/svm-understanding- математика-часть-2/
- https://www.svm-tutorial.com/2015/06/svm-understanding-math-part-3/
- https://www.svm-tutorial.com/2016/09/unconstrained-minimization/
- https://www.svm-tutorial.com/2016/09/convex-functions/
- https://www.svm-tutorial.com/2016/09/duality-lagrange-multipliers/
- Опорный вектор Machines Succinctly by Alexandre Kowalczyk
- Ali Ghodsi, Lec 12: Машина опорных векторов с мягкими краями (SVM)
- https://www.


 1.2 Уравнение идеального разделения
1.2 Уравнение идеального разделения


 -й это была математика, стоящая за моделью SVM.
-й это была математика, стоящая за моделью SVM. 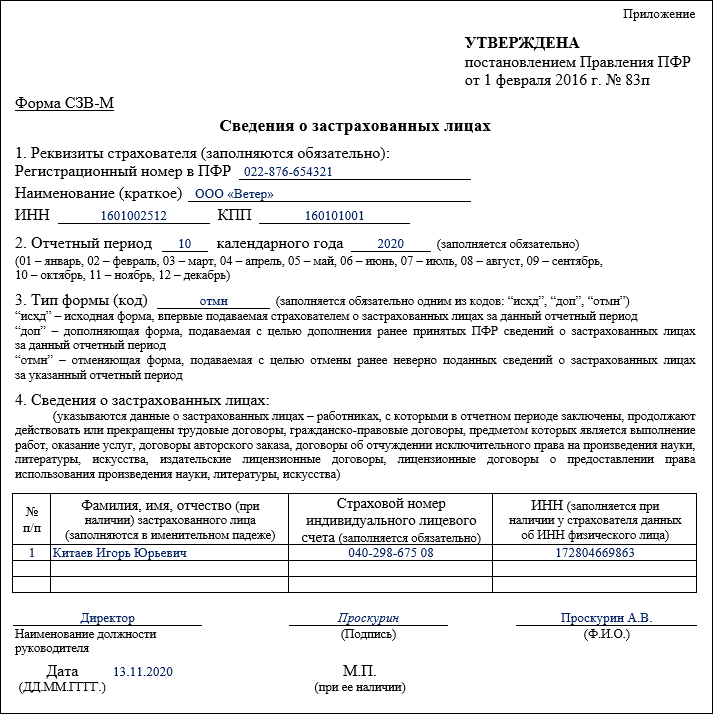 Это было мое понимание задействованной математики в SVM,
и я открыт для предложений относительно моей работы здесь
Это было мое понимание задействованной математики в SVM,
и я открыт для предложений относительно моей работы здесь  .
. Это называется просто Гиперплоскость максимальной маржи . Расстояние между опорными гиперплоскостями называется Margin .
Это называется просто Гиперплоскость максимальной маржи . Расстояние между опорными гиперплоскостями называется Margin .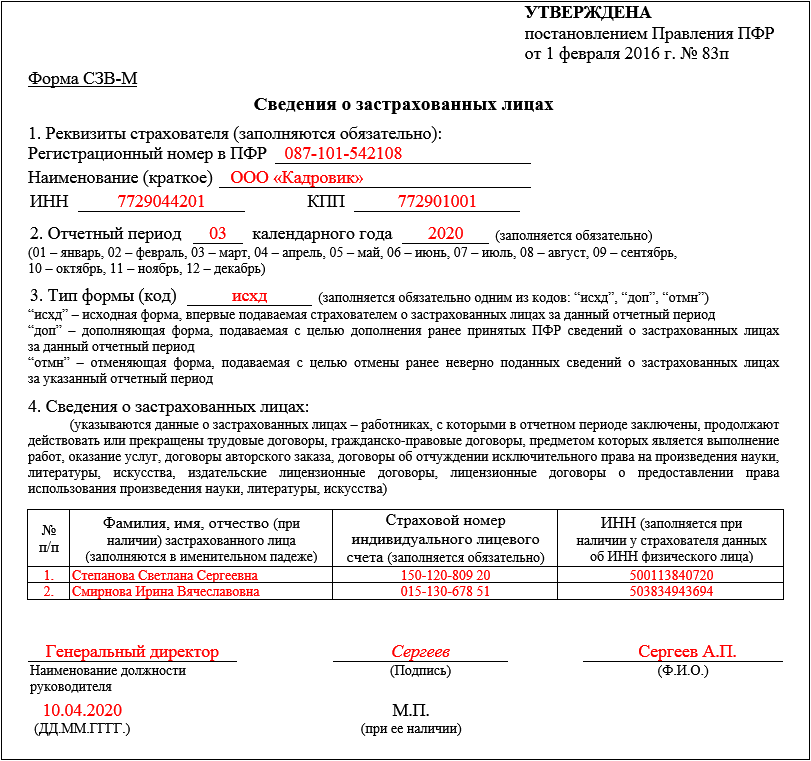


 Вот некоторые из популярных:
Вот некоторые из популярных: то же самое в начале статья).
то же самое в начале статья). x x x x x₀ . 1 и w.x+b=-1 ,
x x x x x₀ . 1 и w.x+b=-1 ,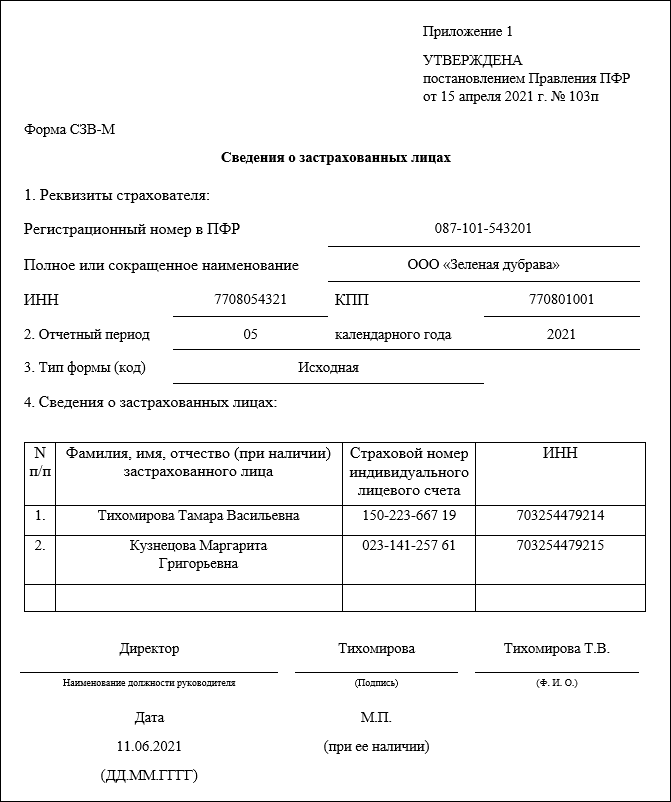 Однако приведенные выше уравнения представляют собой уравнений ограничения неравенства . Таким образом, дополнительный набор условий, называемый условиями Куна — Таккера, также должен удовлетворяться. Мы пройдемся по условиям позже.
Однако приведенные выше уравнения представляют собой уравнений ограничения неравенства . Таким образом, дополнительный набор условий, называемый условиями Куна — Таккера, также должен удовлетворяться. Мы пройдемся по условиям позже. (4)]. Поскольку теперь это учтено, целевой функционал W является новой функцией, которую необходимо оптимизировать вместо уравнения. (3). Это называется ДВОЙНОЙ ФОРМУЛИРОВКОЙ , потому что исходная Целевая функция была изменена!
(4)]. Поскольку теперь это учтено, целевой функционал W является новой функцией, которую необходимо оптимизировать вместо уравнения. (3). Это называется ДВОЙНОЙ ФОРМУЛИРОВКОЙ , потому что исходная Целевая функция была изменена! Бесплатная осуществимость :
Бесплатная осуществимость : Следовательно, нам нужно максимизировать W против αᵢ .
Следовательно, нам нужно максимизировать W против αᵢ .