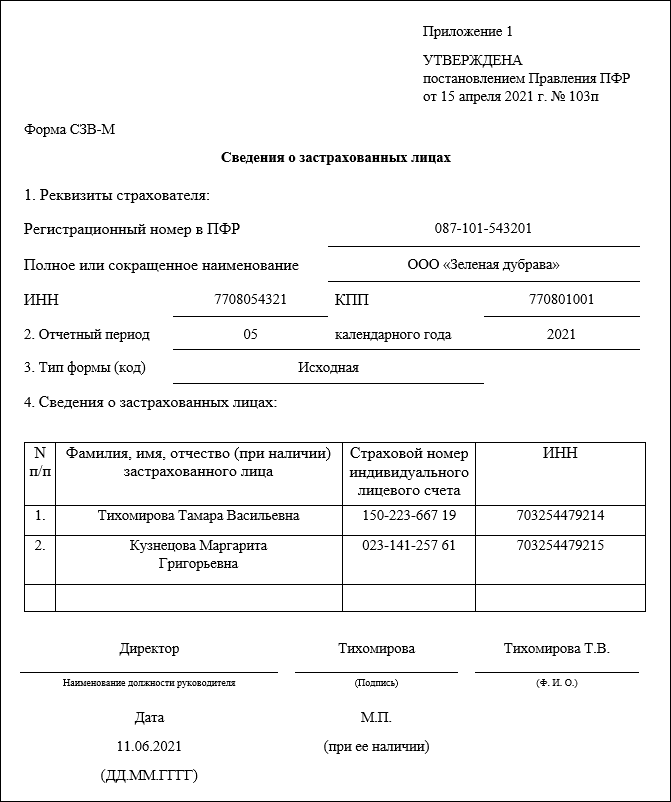
Содержание
SVM Tutorial — Part I · Chris McCormick
Мне было очень трудно получить базовое представление о методах опорных векторов. Чтобы узнать, как работают SVM, я прошел курс Эндрю Нг по машинному обучению (доступен бесплатно в Стэнфорде). Я думаю, что учебники по SVM настолько сложны, потому что обучение SVM — это сложная проблема оптимизации, для объяснения которой требуется много математики и теории.
Однако, просто взглянув на SVM, обученную на простом наборе данных, я думаю, вы можете получить некоторые из наиболее важных сведений о том, как работают SVM.
Я создал очень простой пример SVM, чтобы помочь себе понять некоторые концепции. Я включил сюда результаты и иллюстрации, а также файлы данных, чтобы вы могли запустить алгоритм самостоятельно.
В Excel я создал два набора точек (два «класса»), которые разместил произвольно. Я разместил точки так, чтобы вы могли легко провести прямую линию, чтобы разделить два класса (классы «линейно разделимы»).
Эти точки — мой тренировочный набор, который я использовал для обучения SVM.
Вот электронная таблица Excel, содержащая значения данных и графики в этом посте.
Функция оценки SVM
Обученный метод опорных векторов имеет функцию оценки, которая вычисляет оценку для нового входа. Машина опорных векторов — это бинарный (двухклассовый) классификатор; если результат оценочной функции отрицателен, то вход классифицируется как принадлежащий к классу y = -1. Если оценка положительна, вход классифицируется как относящийся к классу y = 1,9. (i) – это ярлык класса, который имеет одно из двух значений: -1 или 1.
α_i — это коэффициент, связанный с _i_th обучающим примером.
x — это входной вектор, который мы пытаемся классифицировать
K называется функцией ядра.
b — это просто скалярное значение.
Опорные векторы
Вычисление этой функции оценки выглядит очень затратным. Вам нужно будет выполнить операцию над каждой отдельной обучающей точкой только для того, чтобы классифицировать новый ввод x — что, если ваш обучающий набор содержит миллионы точек данных? Как оказалось, коэффициент α_i будет равен нулю для всех точек обучения, кроме «опорных векторов».
На приведенном ниже графике вы можете видеть опорные векторы, выбранные SVM, — три точки обучения, ближайшие к границе решения.
Обучение SVM в WEKA
Для обучения SVM на этом наборе данных я использовал свободно доступный набор инструментов WEKA.
- В проводнике WEKA на вкладке «Предварительная обработка» откройте этот файл .csv, содержащий набор данных.
- На вкладке «Классификация» нажмите кнопку «Выбрать», чтобы выбрать классификатор weka->классификаторы->функции->SMO (SMO — это алгоритм оптимизации, используемый для обучения SVM на наборе данных).
- Нажмите на командную строку классификатора, чтобы открыть диалоговое окно для редактирования аргументов командной строки.
В диалоговом окне измените свойство filterType на «Нет нормализации/стандартизации». Это облегчит интерпретацию результатов.
Также щелкните командную строку свойства «ядро». Это вызовет другое диалоговое окно, позволяющее указать свойства функции ядра. Установите для свойства exponent значение 2.
Примечание для тех, кто уже знаком с ядрами: поскольку наш набор данных линейно разделим, нам не нужен показатель степени 2 в ядре. Однако это необходимо, чтобы заставить WEKA использовать опорные векторы. В противном случае это просто даст вам простое линейное уравнение для функции оценки, что не поможет нам в нашем понимании SVM.
- Нажмите «Старт», чтобы запустить алгоритм обучения.
Ближе к середине вывода вы должны увидеть что-то вроде следующего уравнения:
0,0005 * <7 2 > * Х] - 0,0006 * <9 5 > * Х] + 0,0001 * <4 7 > * Х] + 2,7035
По сути, это функция подсчета очков, которую мы видели в начале поста, но теперь с заполненными значениями.
Числа в угловых скобках — это три опорных вектора <7 2>, <9(я).
Окончательное значение выражения 2,7035 равно b .
Визуализация функции подсчета очков
Теперь мы можем взять наше уравнение подсчета очков:
Подставляем найденные значения, чтобы получить:
Где x1 и x2 — компоненты входного вектора _x _, для которого мы хотим вычислить оценку.
Обратите внимание, что исходное суммирование проводилось по каждой точке обучающей выборки, но мы включили сюда только термины для опорных векторов. Альфа равна нулю для всех остальных точек данных, поэтому эти термины исчезают. 92+2,7035
Измените диапазоны на x: 0–16 и y: 0–16, и вы должны получить что-то вроде следующего:
Функция подсчета очков формирует поверхность в трех измерениях. Там, где он пересекает плоскость z = 0, он образует линию; это наша граница решения. Слева от границы решения входные данные получают оценку выше 0 и присваиваются классу y = 1.
Справа входные данные получают оценку меньше 0 и присваиваются классу y = -1.
В следующем примере мы рассмотрим несколько более сложную задачу классификации, в которой классы не являются линейно разделимыми. В этом примере мы более подробно рассмотрим функцию ядра и то, как она используется для достижения нелинейной классификации.
Включите JavaScript, чтобы просматривать комментарии с помощью Disqus.
Машина опорных векторов · Руководство по программированию UC Business Analytics R
↩
Появление компьютеров привело к быстрому прогрессу в области статистической классификации, одним из которых является машина опорных векторов или SVM. Цель SVM состоит в том, чтобы взять группы наблюдений и построить границы, чтобы предсказать, к какой группе принадлежат будущие наблюдения, на основе их измерений. Различные группы, которые должны быть разделены, будут называться «классами». SVM могут обрабатывать любое количество классов, а также наблюдения любого измерения.
SVM могут принимать практически любую форму (включая линейную, радиальную и полиномиальную, среди прочего) и, как правило, достаточно гибки, чтобы использоваться практически в любой попытке классификации, которую выберет пользователь.
tl;dr
- Требования к репликации: что вам потребуется для воспроизведения анализа в этом руководстве
- Классификатор максимальной маржи: построение строки классификации для полностью разделяемых данных
- Классификаторы опорных векторов: построение линии классификации для неразделимых данных
- Машины опорных векторов: построение границы классификации, линейной или нелинейной, для данных, которые могут быть или не быть разделимыми
- SVM для нескольких классов: методы SVM для более чем 2 классов наблюдений
Требования к репликации
В этом руководстве мы будем использовать пакет tidyverse для обработки данных, пакеты kernlab и e1071 для выполнения вычислений и создания визуализаций, связанных с SVM, и пакет ISLR для загрузки набор данных реального мира и продемонстрировать функциональность машин опорных векторов.
RColorBrewer необходим для создания пользовательской визуализации SVM с использованием kernlab с более чем двумя классами данных. Чтобы обеспечить воспроизводимость результатов, мы явно задаем генератор случайных чисел.
# установить генератор псевдослучайных чисел сет.сид(10) # Прикрепить пакеты library(tidyverse) # обработка и визуализация данных библиотека (kernlab) # методология SVM библиотека (e1071) # методология SVM library(ISLR) # содержит пример набора данных "Khan" library(RColorBrewer) # настраиваемая окраска графиков
Наборы данных, используемые в руководстве (за исключением Khan ), будут созданы с помощью встроенных команд R. Методология метода опорных векторов хороша для любого количества измерений, но ее трудно визуализировать для более чем 2. Как упоминалось ранее, SVM устойчивы для любого количества классов, но мы будем придерживаться не более 3-х на протяжении этого курса. руководство.
Классификатор максимальной маржи
Если классы разделены линейной границей, мы можем использовать Классификатор максимальной маржи , чтобы найти границу классификации.
Чтобы визуализировать пример разделенных данных, мы генерируем 40 случайных наблюдений и назначаем их двум классам. При визуальном осмотре мы видим, что существует бесконечно много линий, разделяющих два класса.
# Набор данных для создания выборки - полностью разделен
x <- матрица (rнорма (20*2), ncol = 2)
у <- с (повтор (-1,10), повтор (1,10))
х[у==1,] <- х[у==1,] + 3/2
dat <- data.frame(x=x, y=as.factor(y))
# Данные графика
ggplot (данные = dat, aes (x = x.2, y = x.1, цвет = y, форма = y)) +
geom_point (размер = 2) +
scale_color_manual (значения = c ("# 000000", "# FF0000")) +
тема (легенда.позиция = "нет")
Целью классификатора максимального поля является определение линейной границы, которая максимизирует общее расстояние между линией и ближайшей точкой в каждом классе. Мы можем использовать функцию svm() в пакете e1071 , чтобы найти эту границу.
# Подгонка модели опорного вектора к набору данных svmfit <- svm(y~.
, data = dat, kernel = "linear", scale = FALSE)
# Результаты графика
сюжет (svmfit, дат)
На графике точки, обозначенные «X», являются опорные векторы , или точки, непосредственно влияющие на классификационную линию. Точки, отмеченные знаком «о», — это другие точки, которые не влияют на расчет линии. Этот принцип заложит основу для машин опорных векторов. Тот же график можно создать с помощью пакета kernlab со следующими результатами:
# подгонка модели и создание графика kernfit <- ksvm(x, y, type = "C-svc", kernel = 'vanilladot') график (кернфит, данные = х)
kernlab показывает немного больше деталей, чем e1071 , показывая цветовой градиент, который указывает, насколько уверенно будет классифицироваться новая точка на основе ее признаков. Как и на первом графике, опорные векторы отмечены, в данном случае, как закрашенные точки, а классы обозначены разными фигурами.
Классификаторы опорных векторов
Как бы ни был удобен для понимания максимальный предельный классификатор, большинство реальных наборов данных не могут быть полностью разделены линейной границей.
Для обработки таких данных мы должны использовать модифицированную методологию. Мы моделируем новый набор данных, в котором классы более смешанные.
# Построение выборочного набора данных - не полностью разделен
x <- матрица (rнорма (20*2), ncol = 2)
у <- с (повтор (-1,10), повтор (1,10))
х[у==1,] <- х[у==1,] + 1
dat <- data.frame(x=x, y=as.factor(y))
# Набор данных графика
ggplot (данные = dat, aes (x = x.2, y = x.1, цвет = y, форма = y)) +
geom_point (размер = 2) +
scale_color_manual (значения = c ("# 000000", "# FF0000")) +
тема (легенда.позиция = "нет")
Независимо от того, являются ли данные разделяемыми или нет, синтаксис команды svm() одинаков. Однако в случае данных, которые не являются линейно разделимыми, стоимость = аргумент приобретает реальное значение. Это количественно определяет штраф, связанный с наличием наблюдения на неправильной стороне границы классификации. Мы можем построить подгонку так же, как и в случае полностью отделимого случая.
Сначала мы используем e1071 :
# Подгонка модели опорного вектора к набору данных svmfit <- svm(y~., data = dat, kernel = "linear", cost = 10) # Результаты графика сюжет (svmfit, дат)
Увеличив стоимость неправильной классификации с 10 до 100, вы увидите разницу в строке классификации. Мы повторяем процесс построения SVM, используя kernlab package:
# Подгонка модели опорного вектора к набору данных kernfit <- ksvm(x,y, type = "C-svc", kernel = 'vanilladot', C = 100) # Результаты графика график (кернфит, данные = х)
Но как определить, насколько дорого обходятся эти ошибочные классификации? Вместо указания стоимости заранее мы можем использовать функцию tune() из e1071 , чтобы протестировать различные затраты и определить, какое значение дает наиболее подходящую модель.
# найти оптимальную стоимость неправильной классификации
tune.out <- tune(svm, y~., data = dat, kernel = "linear",
диапазоны = список (стоимость = c (0,001, 0,01, 0,1, 1, 5, 10, 100)))
# извлечь лучшую модель
(bestmod <- tune. out$best.model)
##
## Вызов:
## best.tune(method = svm, train.x = y ~ ., data = dat, ranges = list(cost = c(0,001,
## 0.01, 0.1, 1, 5, 10, 100)), ядро = "линейный")
##
##
## Параметры:
## Тип SVM: C-классификация
## SVM-ядро: линейный
## стоимость: 0,1
## гамма: 0,5
##
## Количество опорных векторов: 16
out$best.model)
##
## Вызов:
## best.tune(method = svm, train.x = y ~ ., data = dat, ranges = list(cost = c(0,001,
## 0.01, 0.1, 1, 5, 10, 100)), ядро = "линейный")
##
##
## Параметры:
## Тип SVM: C-классификация
## SVM-ядро: линейный
## стоимость: 0,1
## гамма: 0,5
##
## Количество опорных векторов: 16
Для нашего набора данных оптимальная стоимость (из предоставленных нами вариантов) рассчитывается как 0,1, что не сильно наказывает модель за неправильно классифицированные наблюдения. Как только эта модель будет идентифицирована, мы можем построить таблицу предсказанных классов против истинных классов, используя команду predict() следующим образом:
# Создать таблицу ошибочно классифицированных наблюдений ypred <- предсказать(bestmod, dat) (misclass <- table(predict = ypred, правда = dat$y)) ## правда ## предсказать -1 1 ## -1 93 ## 1 1 7
Используя этот классификатор опорных векторов, 80% наблюдений были правильно классифицированы, что соответствует тому, что мы видим на графике.
Если бы мы хотели протестировать наш классификатор более строго, мы могли бы разделить наши данные на наборы для обучения и тестирования, а затем посмотреть, как наш SVC работает с наблюдениями, не используемыми для построения модели. Мы будем использовать этот метод обучения и тестирования позже в этом руководстве для проверки наших SVM.
Машины опорных векторов
Классификаторы опорных векторов являются подмножеством группы структур классификации, известных как Машины опорных векторов . Машины опорных векторов могут строить границы классификации, которые имеют нелинейную форму. Варианты классификации структур с помощью команды svm() из пакета e1071 : линейная, полиномиальная, радиальная и сигмовидная. Чтобы продемонстрировать нелинейную границу классификации, мы построим новый набор данных.
# построить больший набор случайных данных x <- матрица (rнорма (200*2), ncol = 2) х[1:100,] <- х[1:100,] + 2,5 х[101:150,] <- х[101:150,] - 2,5 у <- с (повтор (1,150), повтор (2,50)) dat <- data.
frame(x=x,y=as.factor(y))
# Данные графика
ggplot (данные = dat, aes (x = x.2, y = x.1, цвет = y, форма = y)) +
geom_point (размер = 2) +
scale_color_manual (значения = c ("# 000000", "# FF0000")) +
тема (легенда.позиция = "нет")
Обратите внимание, что данные не являются линейно разделимыми и, кроме того, не все сгруппированы вместе в одной группе. Есть два раздела наблюдений класса 1 с кластером наблюдений класса 2 между ними. Чтобы продемонстрировать мощь SVM, мы возьмем 100 случайных наблюдений из набора и используем их для построения нашей границы. Мы устанавливаем ядро = «радиальное» на основе формы наших данных и отображаем результаты.
# установить генератор псевдослучайных чисел сет.сид(123) # пример обучающих данных и подходящая модель train <- base::sample(200 100, replace = FALSE) svmfit <- svm(y~., data = dat[train,], kernel = "radial", gamma = 1, cost = 1) # классификатор сюжетов сюжет (svmfit, дат)
Ту же процедуру можно выполнить с помощью пакета kernlab , который имеет гораздо больше параметров ядра , чем соответствующая функция в e1071 .
В дополнение к четырем вариантам в e1071 этот пакет позволяет использовать гиперболический тангенс, лапласиан, бессель, сплайн, струну или ядро ANOVA RBF. Чтобы соответствовать этим данным, мы установили стоимость такой же, как и раньше, 1.
# Подгонка радиального SVM в kernlab kernfit <- ksvm(x[train,],y[train], type = "C-svc", kernel = 'rbfdot', C = 1, scaled = c()) # График данных обучения график (кернфит, данные = х [поезд,])
Мы видим, что, по крайней мере визуально, SVM неплохо разделяет два класса. Чтобы подогнать модель, мы использовали 90 195 стоимость = 1 , но, как упоминалось ранее, обычно не очевидно, какая стоимость даст оптимальную границу классификации. Мы можем использовать команду tune() , чтобы попробовать несколько разных значений стоимости, а также несколько разных значений параметра масштабирования, используемого для соответствия нелинейным границам.
# настроить модель, чтобы найти оптимальную стоимость, значения гаммы tune.
out <- tune(svm, y~., data = dat[train,], kernel = "radial",
диапазоны = список (стоимость = c (0,1,1,10,100,1000),
гамма = с(0,5,1,2,3,4)))
# показать лучшую модель
настроить.из $лучшая.модель
##
## Вызов:
## best.tune(method = svm, train.x = y ~ ., data = dat[train, ],
## ranges = list(cost = c(0,1, 1, 10, 100, 1000), gamma = c(0,5,
## 1, 2, 3, 4)), ядро = "радиальное")
##
##
## Параметры:
## Тип SVM: C-классификация
## SVM-ядро: радиальное
## стоимость: 1
## гамма: 0,5
##
## Количество опорных векторов: 34
Модель, которая максимально уменьшает ошибку в обучающих данных, использует стоимость 1 и значение 0,5. Теперь мы можем увидеть, насколько хорошо работает SVM, предсказав класс 100 тестовых наблюдений:
# проверка производительности модели
(действительно <- таблица (true = dat [-train, "y"], pred = предсказать (tune.out $ best.model,
newx = dat[-поезд,])))
## пред
## правда 1 2
## 1 58 19
## 2 16 7
Наша наиболее подходящая модель обеспечивает 65% точность определения классов.
Для такой сложной формы наблюдений это сработало достаточно хорошо. Мы можем оспорить этот метод, добавив дополнительные классы наблюдений.
SVM для нескольких классов
Процедура не меняется для наборов данных, которые включают более двух классов наблюдений. Мы создаем наш набор данных так же, как и раньше, только теперь указываем три класса вместо двух:
# построить набор данных
x <- rbind (x, матрица (rnorm (50 * 2), ncol = 2))
у <- с (у, представитель (0,50))
х[у==0,2] <- х[у==0,2] + 2,5
dat <- data.frame(x=x, y=as.factor(y))
# набор данных графика
ggplot (данные = dat, aes (x = x.2, y = x.1, цвет = y, форма = y)) +
geom_point (размер = 2) +
scale_color_manual (значения = c ("# 000000", "# FF0000", "# 00BA00")) +
тема (легенда.позиция = "нет")
Команды не меняются для пакета e1071 . Мы указываем стоимость и параметр настройки и подбираем машину опорных векторов. Результаты и интерпретация аналогичны двухклассовой классификации.
# подходит для модели svmfit <- svm(y~., data = dat, kernel = "radial", cost = 10, gamma = 1) # результат графика сюжет (svmfit, дат)
Мы можем проверить, насколько хорошо наша модель соответствует данным, с помощью команды predict() следующим образом:
#построить таблицу ypred <- прогнозировать (svmfit, dat) (misclass <- table(predict = ypred, правда = dat$y)) ## правда ## предсказать 0 1 2 ## 0 38 2 4 ## 1 8 143 4 ## 2 4 5 42
Как показано в результирующей таблице, 89% наших тренировочных наблюдений были правильно классифицированы. Однако, поскольку мы не разбивали наши данные на наборы для обучения и тестирования, мы не проверяли наши результаты по-настоящему.
Пакет kernlab , с другой стороны, может соответствовать более чем 2 классам, но не может отображать результаты. Чтобы визуализировать результаты ksvm , мы выполняем шаги, перечисленные ниже, чтобы создать сетку точек, предсказать значение каждой точки и построить результаты:
# подгонка и построение графика kernfit <- ksvm(as.
matrix(dat[2:1]),dat$y, type = "C-svc", kernel = 'rbfdot',
C = 100, в масштабе = c())
# Создайте мелкую сетку пространства признаков
x.1 <- seq(from = min(dat$x.1), to = max(dat$x.1), length = 100)
x.2 <- seq(from = min(dat$x.2), to = max(dat$x.2), length = 100)
x.grid <- расширить.grid (x.2, x.1)
# Получить прогнозы классов по сетке
pred <- прогнозировать (kernfit, newdata = x.grid)
# Отобразить результаты
cols <- brewer.pal(3, "Set1")
сюжет (x.grid, pch = 19, столбец = настроить цвет (столбцы [пред], alpha.f = 0,05))
классы <- матрица (пред, nrow = 100, ncol = 100)
контур (x = x.2, y = x.1, z = классы, уровни = 1:3, метки = "", добавить = TRUE)
точки(dat[ 2:1], pch = 19, col = cols[predict(kernfit)])
Приложение
Набор данных Khan содержит данные о 83 образцах тканей с 2308 измерениями экспрессии генов в каждом образце. Они были разделены на 63 обучающих наблюдения и 20 проверочных наблюдений, и в наборе есть четыре различных класса.
Визуализировать такие данные было бы невозможно, поэтому для построения нашей модели выбираем самый простой классификатор (линейный). Мы будем использовать 9Команда 0195 svm от e1071 для проведения нашего анализа.
# подходит для модели dat <- data.frame(x = Khan$xtrain, y=as.factor(Khan$ytrain)) (out <- svm(y~., data = dat, kernel = "linear", cost=10)) ## ## Вызов: ## svm(formula = y ~ ., data = dat, kernel = "linear", cost = 10) ## ## ## Параметры: ## Тип SVM: C-классификация ## SVM-ядро: линейный ## стоимость: 10 ## гамма: 0.0004332756 ## ## Количество опорных векторов: 58
Прежде всего, мы можем проверить, насколько хорошо наша модель справилась с классификацией тренировочных наблюдений. Обычно это высокое значение, но опять же, оно не подтверждает правильность модели. Если модель не очень хорошо классифицирует тренировочный набор, это может быть красным флажком. В нашем случае все 63 обучающих наблюдения были правильно классифицированы.
# проверить производительность модели на тренировочном наборе стол (с $ приспособленным, dat $ y) ## ## 1 2 3 4 ## 1 8 0 0 0 ## 2 0 23 0 0 ## 3 0 0 12 0 ## 4 0 0 0 20
Чтобы выполнить проверку, мы можем проверить, как модель работает на тестовом наборе:
# проверить производительность модели
dat.
