Сзв м новая форма с июля 2018: Нужно ли сдавать нулевой СЗВ-М

Содержание

Отчетность в программах 1С: Предприятие

Информация о материале

И снова здравствуйте. В новый год с новыми отчетами. На это раз порадовал нас и ФСС. С  1 января 2022 года при приеме на работу сотрудника работодателю необходимо в течение 3 дней предоставить в ФСС сведения, которые необходимы для перечисления ему пособия. Сведения должны содержать ФИО сотрудника, дату рождения, СНИЛС, ИНН (при наличии), а также способ перечисления и реквизиты либо отметку о  том, что физическое лицо не является сотрудником организации. Кроме того, при изменении каких-либо переданных в ФСС сведений, также необходимо отправить сведения в ФСС.

Информация о материале

Здравствуйте, мои дорогие бухгалтеры. Сегодня хочу предложить вам следующую тему для разговора – Безопасная доля вычетов по НДС и как программа 1С:Бухгалтерия 8.3 поможет нам ее контролировать.
Сначала несколько слов о том, что же такое Безопасная доля вычетов. Такого понятия в Налоговом кодексе РФ нет, но, тем не менее, это показатель, превышение которого может привлечь внимание налоговых органов к организации. Есть две основные величины, которые использует ФНС:

Информация о материале

Ну вот и наступила очередная отчетная компания.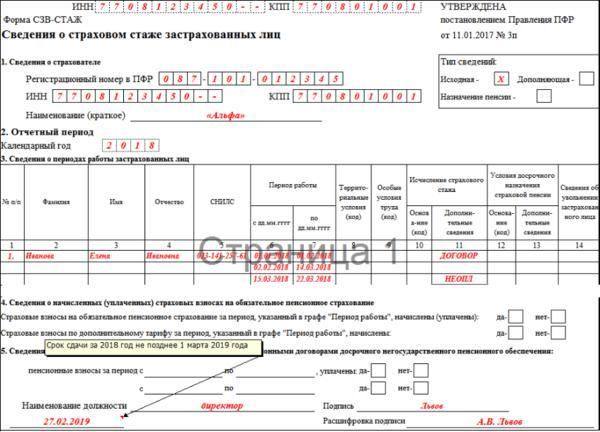 Особенность ее в том, что теперь уже все пользователи программы 1С:ЗУП 8 перешли на работу в программе новой редакции. В связи с этим мы решили обновить свою старую статью по заполнению регламентированной отчетности в ФСС и помочь вам разобраться с этим отчетом в новой программе.

Информация о материале

Все организации, работающие на общей системе налогообложения, должны вести налоговый учет по налогу на прибыль в аналитических регистрах налогового учета, формы которых разрабатываются налогоплательщиком самостоятельно и должны быть включены в приложения к учетной политике по налоговому учету.

  • Бухгалтерия 3.0

Информация о материале

Сегодня я хочу рассказать вам о заполнении в 1С:Зарплата и управление персоналом еще одного отчета – отчета по форме СЗВ-К.
«Пенсионный» просит работодателей предоставить такой отчет на тех работников, на кого в их базе отсутствуют сведения о трудовом стаже до 2002 г. И в последнее время уже несколько наших клиентов обратились к нам с просьбой о помощи в заполнении этой формы, поэтому мы решили раскрыть эту тему на нашем сайте.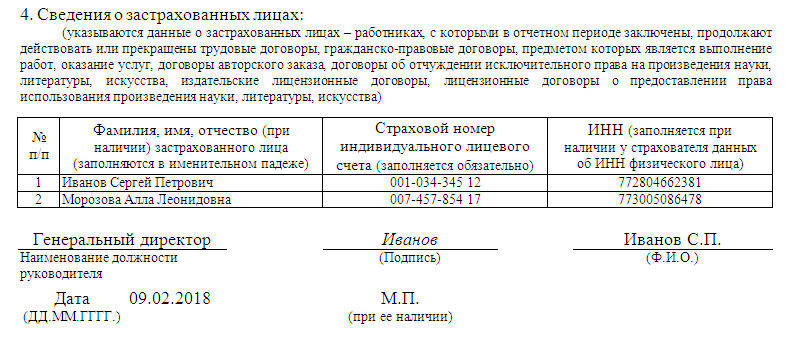

  • Бухгалтерия 3.0

  • ЗУП 3.1

  • ЗУП 2.5

Информация о материале

Чем ближе конец июля тем больше различных вопросов по отчетности возникает у наших клиентов. И вот один из последних хитов в списке различных проблем: после сдачи расчета по страховым взносам выяснилось, что одна из сотрудниц поменяла фамилию, а предупредить об этом отдел кадров «забыла», и как следствие налоговая просит прислать корректировочный расчет с уточнением по одной этой сотруднице.

Информация о материале

Как заполняется декларация по налогу на прибыль в программе 1С: Бухгалтерия предприятия? Откуда программа берет данные для заполнения декларации? Почему сведения в декларации не совпадают с ОСВ? Ответы на эти вопросы вы узнаете из нашей новой статьи.

  • Бухгалтерия 3.0

  • Бухгалтерия 2. 0

Информация о материале

Новый отчет по форме СЗВ-СТАЖ. Некоторые бухгалтера уже сейчас столкнулись с необходимость его сдачи. Где он находится и как заполняется узнаете из нашей новой статьи.

  • Бухгалтерия 3.0

  • ЗУП 3.1

  • ЗУП 2.5

  • Бухгалтерия 2.0

Информация о материале

 

Расчет по страховым взносам – новый отчет в жизни бухгалтера. Где он находится в различных программах 1С и как заполняется в 1C:Бухгалтерия 8, ред. 3, попробуем вместе разобраться в моей новой статье.

  • Бухгалтерия 3.0

  • ЗУП 3.1

  • ЗУП 2.5

  • Бухгалтерия 2.0

Информация о материале

Не заполняются коды ОКВЭД в отчетности в РСВ-1 за 2016 год, не встает код ОКВЭД в сведениях о среднесписочной численности работников за 2016 год. Такие вопросы наши специалисты слышат ежедневно с начала рабочего 2017 года. Многие бухгалтеры хотят поскорее сдать отчетность и поэтому мы решили поспешить вам на помощь и объяснить, как и что надо сделать в различных программах 1С для заполнения этого реквизита в отёчности.

  • Бухгалтерия 3.0

  • ЗУП 3.1

  • ЗУП 2. 5

  • Бухгалтерия 2.0

Информация о материале

Уважаемые коллеги. Отчетная кампания не была бы так интересна и увлекательна для бухгалтера, если бы не ежеквартальные изменения в формах отчетности. Наш центр напоминает вам, что с 1 июля 2016 года был изменен перечень кодов для операций, которые указываются в книге покупок и книге продаж для расчета НДС.

  • НДС

Информация о материале

Добрый день, коллеги. Быстро пролетело лето, а за ним и сентябрь. И вот опять перед бухгалтерами возник отчет по форме 6-НДФЛ. И хоть до конца месяца еще немало времени и возможно выйдет в свет еще не одно обновление программ 1С, я решила все-таки попробовать сформировать отчетность за 9 месяцев.

  • 6 НДФЛ

  • ЗУП 3.1

Информация о материале

Добрый день, дорогие коллеги. Давненько я не радовала вас своими сообщениями на тему: «Что и где лежит в программах 1С и как это найти?»

В этом году бухгалтерам добавилось работы с новыми формами отчетности

  • 6 НДФЛ

  • ЗУП 3.1

  • СЗВ-М

Информация о материале

Добрый день, мои дорогие коллеги. Вот и наступило время для сдачи отчетности по форме 6-НДФЛ за второй квартал 2016 года. Этот отчет на мой взгляд, является одним из самых проблематичных на сегодняшний день.

  • 6 НДФЛ

  • ЗУП 2.5

Информация о материале

Добрый день, дорогие наши читатели, коллеги, партнеры и пользователи программ 1С. С вами опять ваш консультант Виктория.

Сегодня я хочу еще раз поговорить с Вами о простой и загадочной отчетности в ПФР.

  • СЗВ-М

  • ЗУП 2. 5

Информация о материале

В связи с тем, что периодичность отчетности в контролирующие органы все уменьшается, а количество и разновидность отчетов неуклонно растет, то выбор системы электронной отчетности вопрос весьма актуальный.

Информация о материале

 Продолжая тему СЗВ-М, начатую в предыдущих статьях (ссылки укажем в конце статьи), мы совсем забыли о конфигурациях 1С7. 7 и сегодня мы решили исправить этот недочет. Искать форму СЗВ-М в 1с 7.7 мы будем в двух конфигурациях 1С 7.7 УСН (Упрощенная система налогообложения) и ЗиК (Зарплата и Кадры). Все примеры из УСН также подходят к Бухгалтерии 7.7. Итак, начнем.

  • СЗВ-М

  • 1С 7.7

Информация о материале

 

Здравствуйте, коллеги. Я к вам с новой статьей. Последнее время участились вопросы, связанные с отражением доходов в виде материальной выгоды и НДФЛ в расчете 6-НДФЛ.

  • 6 НДФЛ

  • ЗУП 2.5

Информация о материале

 

Дорогие коллеги! Последнее время очень часто нам звонят с вопросом: «Вышла ли новая форма СЗВ-М и если да, то где ее искать в программах 1С?» В связи с этим мы решили написать небольшую заметку на эту тему.

  • Бухгалтерия 3. 0

  • ЗУП 3.1

  • СЗВ-М

  • ЗУП 2.5

  • Бухгалтерия 2.0

Информация о материале

 Добрый день, дорогие мои друзья. Наконец то вышло долгожданное обновление программы 1С Зарплата и управление персоналом 2.5, в котором заявлено много изменений, связанных с улучшением заполнения формы 6-НДФЛ. Ну что ж, приступим.

  • 6 НДФЛ

  • ЗУП 2. 5

Информация о материале

Дорогие мои друзья, клиенты и просто случайные гости нашего сайта! Сегодня я постараюсь рассказать вам о своем опыте заполнения новой для всех нас отчетности по форме 6-НДФЛ.

  • 6 НДФЛ

  • ЗУП 2.5

Информация о материале

Начало 16 года встречаем тотальным наблюдением!
Дело в том, что раз в пять лет органы Госстатистики проводят стат. наблюдение (мониторинг ) субъектов бизнеса. Будь-то ИП или организация. Последнее было в 2011 году.

Информация о материале

Министерством труда были внесены корректировки в расчет по форме 4-ФСС, а также уточнен порядок его заполнения.

Изменения направлены на приведение отчета в соответствие с действующим законодательством, в частности, внесены следующие поправки:

  • 4-ФСС

Информация о материале

 Сегодня мы рассмотрим на первый взгляд не очень сложный вопрос, но тем не менее, при получении из налоговой требования сделать корректировку по НДФЛ, у

  • Бухгалтерия 3.0

  • ЗУП 2.5

  • 2-НДФЛ

Информация о материале

В период сдачи отчетности в ПФР в течение 2015 года мы выяснили, что достаточно часто возникает такая ситуация, когда после предоставления расчета по форме РСВ-1 требуется его пересдача.

  • ЗУП 2.5

  • Перс.учет

Машины опорных векторов для машинного обучения

[Новая книга] Нажмите, чтобы получить модели строительных трансформаторов с вниманием !

Используйте код предложения 20offearlybird , чтобы получить скидку 20%.

Джейсон Браунли on 20 апреля 2016 г. в Алгоритмы машинного обучения

Последнее обновление: 15 августа 2020 г.

Support Vector Machines, пожалуй, один из самых популярных и обсуждаемых алгоритмов машинного обучения.

Они были чрезвычайно популярны примерно в то время, когда они были разработаны в 1990-х годах, и по-прежнему остаются популярным методом высокопроизводительного алгоритма с небольшой настройкой.

В этом посте вы познакомитесь с алгоритмом машинного обучения машины опорных векторов (SVM). После прочтения этого поста вы будете знать:

  • Как распутать множество названий, используемых для обозначения машин опорных векторов.
  • Представление, используемое SVM, когда модель фактически хранится на диске.
  • Как можно использовать изученное представление модели SVM для прогнозирования новых данных.
  • Как изучить модель SVM на основе обучающих данных.
  • Как лучше всего подготовить данные для алгоритма SVM.
  • Где можно найти дополнительную информацию об SVM.

SVM — захватывающий алгоритм с относительно простыми концепциями. Этот пост был написан для разработчиков, которые практически не имеют опыта работы со статистикой и линейной алгеброй.

Таким образом, мы останемся в этом описании на высоком уровне и сосредоточимся на конкретных проблемах реализации. Вопрос о том, почему используются определенные уравнения или как они были получены, не рассматривается, и вы можете углубиться в раздел дополнительной литературы.

Начните свой проект с моей новой книги Master Machine Learning Algorithms, включающей пошаговых руководства и файлы электронных таблиц Excel для всех примеров.

Начнем.

Машины опорных векторов для машинного обучения
Фото Франсиско Барбериса, некоторые права защищены.

Классификатор максимальной маржи

Классификатор максимальной маржи — это гипотетический классификатор, который лучше всего объясняет, как SVM работает на практике.

Числовые входные переменные (x) в ваших данных (столбцах) образуют n-мерное пространство. Например, если бы у вас было две входные переменные, это сформировало бы двумерное пространство.

Гиперплоскость — это линия, разделяющая пространство входных переменных. В SVM гиперплоскость выбирается для лучшего разделения точек в пространстве входных переменных по их классу, либо классу 0, либо классу 1. В двух измерениях вы можете визуализировать это как линию, и давайте предположим, что все наши входные точки могут быть полностью разделены этой линией. Например:

В0 + (В1 * Х1) + (В2 * Х2) = 0

Где коэффициенты (B1 и B2), определяющие наклон линии и точку пересечения (B0), определяются алгоритмом обучения, а X1 и X2 являются двумя входными переменными.

С помощью этой строки можно делать классификации. Подставляя входные значения в уравнение линии, вы можете вычислить, находится ли новая точка выше или ниже линии.

  • Над линией уравнение возвращает значение больше 0, и точка принадлежит к первому классу (классу 0).
  • Ниже линии уравнение возвращает значение меньше 0, и точка принадлежит второму классу (классу 1).
  • Значение, близкое к линии, возвращает значение, близкое к нулю, и точку может быть трудно классифицировать.
  • Если величина значения велика, модель может быть более уверенной в прогнозе.

Расстояние между линией и ближайшими точками данных называется границей. Наилучшей или оптимальной линией, которая может разделить два класса, является линия с наибольшим запасом. Это называется гиперплоскостью максимального запаса.

Поле рассчитывается как перпендикулярное расстояние от линии только до ближайших точек. Только эти точки имеют значение при определении линии и построении классификатора. Эти точки называются опорными векторами. Они поддерживают или определяют гиперплоскость.

Гиперплоскость изучается на основе обучающих данных с использованием процедуры оптимизации, которая максимизирует запас.

Получите БЕСПЛАТНУЮ интеллект-карту алгоритмов

Образец удобной интеллект-карты алгоритмов машинного обучения.

Я создал удобную интеллект-карту из 60+ алгоритмов, организованных по типам.

Скачайте, распечатайте и пользуйтесь.

Также получите эксклюзивный доступ к мини-курсу по алгоритмам машинного обучения по электронной почте.

 

 

Классификатор мягкой маржи

На практике реальные данные беспорядочны и не могут быть идеально разделены с помощью гиперплоскости.

Необходимо ослабить ограничение максимального отступа линии, разделяющей классы. Это часто называют классификатором мягкой маржи. Это изменение позволяет некоторым точкам в обучающих данных нарушать разделительную линию.

Вводится дополнительный набор коэффициентов, дающих марже пространство для маневра в каждом измерении. Эти коэффициенты иногда называют резервными переменными. Это увеличивает сложность модели, так как у модели есть больше параметров, которые можно подобрать к данным, чтобы обеспечить эту сложность.

Введен параметр настройки, называемый просто C, который определяет величину покачивания, разрешенного во всех измерениях. Параметры C определяют количество нарушений допустимой маржи. C=0 не является нарушением, и мы возвращаемся к негибкому классификатору максимальной маржи, описанному выше. Чем больше значение C, тем больше разрешено нарушений гиперплоскости.

Во время обучения гиперплоскости на основе данных все обучающие экземпляры, находящиеся в пределах расстояния от поля, будут влиять на размещение гиперплоскости и называются опорными векторами. И поскольку C влияет на количество экземпляров, которым разрешено попадать в пределы, C влияет на количество векторов поддержки, используемых моделью.

  • Чем меньше значение C, тем более чувствителен алгоритм к обучающим данным (более высокая дисперсия и меньшее смещение).
  • Чем больше значение C, тем менее чувствителен алгоритм к обучающим данным (меньшая дисперсия и большее смещение).

Машины опорных векторов (ядра)

Алгоритм SVM реализован на практике с использованием ядра.

Изучение гиперплоскости в линейном SVM выполняется путем преобразования задачи с использованием некоторой линейной алгебры, что выходит за рамки этого введения в SVM.

Мощным открытием является то, что линейный SVM можно перефразировать, используя внутренний продукт любых двух заданных наблюдений, а не сами наблюдения. Внутренний продукт между двумя векторами представляет собой сумму произведений каждой пары входных значений.

Например, скалярное произведение векторов [2, 3] и [5, 6] равно 2*5 + 3*6 или 28.

Уравнение для прогнозирования новых входных данных с использованием скалярного произведения между входными данными (x) и каждым опорным вектором (xi) вычисляется следующим образом:

f(x) = B0 + сумма(ai * (x,xi))

Это уравнение включает вычисление внутренних произведений нового входного вектора (x) со всеми опорными векторами в обучающих данных. Коэффициенты B0 и ai (для каждого входа) должны быть оценены из обучающих данных алгоритмом обучения.

Линейное ядро ​​SVM

Скалярный продукт называется ядром и может быть переписан как:

К(х, хи) = сумма(х * хи)

Ядро определяет сходство или меру расстояния между новыми данными и опорными векторами. Скалярный продукт — это мера подобия, используемая для линейного SVM или линейного ядра, поскольку расстояние представляет собой линейную комбинацию входных данных.

Можно использовать другие ядра, преобразующие входное пространство в более высокие измерения, такие как полиномиальное ядро ​​и радиальное ядро. Это называется трюк с ядром. 92))

Где гамма — это параметр, который необходимо указать для алгоритма обучения. Хорошим значением по умолчанию для гаммы является 0,1, где гамма часто бывает 0 < гамма < 1. Радиальное ядро ​​очень локально и может создавать сложные области в пространстве признаков, например замкнутые полигоны в двумерном пространстве.

Как изучить модель SVM

Модель SVM необходимо решить с помощью процедуры оптимизации.

Вы можете использовать процедуру численной оптимизации для поиска коэффициентов гиперплоскости. Это неэффективно и не является подходом, используемым в широко используемых реализациях SVM, таких как LIBSVM. Если реализовать алгоритм в качестве упражнения, вы можете использовать стохастический градиентный спуск.

Существуют специализированные процедуры оптимизации, которые переформулируют задачу оптимизации как задачу квадратичного программирования. Наиболее популярным методом подбора SVM является метод последовательной минимальной оптимизации (SMO), который очень эффективен. Он разбивает проблему на подзадачи, которые можно решить аналитически (вычисляя), а не численно (путем поиска или оптимизации).

Подготовка данных для SVM

В этом разделе перечислены некоторые рекомендации по лучшей подготовке обучающих данных при изучении модели SVM.

  • Числовые входы : SVM предполагает, что ваши входы являются числовыми. Если у вас есть категориальные входные данные, вам может потребоваться преобразовать их в бинарные фиктивные переменные (по одной переменной для каждой категории).
  • Двоичная классификация : базовая SVM, описанная в этом посте, предназначена для задач бинарной (двухклассовой) классификации. Хотя были разработаны расширения для регрессии и многоклассовой классификации.

Дополнительная литература

Машины опорных векторов — это огромная область изучения. На эту тему существует множество книг и статей. В этом разделе перечислены некоторые основополагающие и наиболее полезные результаты, если вы хотите глубже погрузиться в предысторию и теорию техники.

У Владимира Вапника, одного из изобретателей этой техники, есть две книги, которые считаются основополагающими по этой теме. Они очень математические, а также строгие.

  • Природа статистической теории обучения, Вапник, 1995
  • Статистическая теория обучения, Вапник, 1998

Любая хорошая книга по машинному обучению будет посвящена SVM, ниже приведены некоторые из моих любимых.

  • Введение в статистическое обучение: с приложениями в R, глава 8
  • Прикладное прогнозное моделирование, глава 13
  • Элементы статистического обучения: интеллектуальный анализ данных, вывод и прогнозирование Глава 12

Существует множество руководств и журнальных статей по SVM. Ниже приведена ссылка на основополагающую статью Кортеса и Вапника по SVM, а также на отличный вводный учебник.

  • Сети опорных векторов [PDF] Кортеса и Вапника 1995
  • Учебное пособие по методам опорных векторов для распознавания образов [PDF] 1998

В Википедии есть хорошая (хотя и неполная) информация по теме:

  • Метод опорных векторов в Википедии
  • Викиучебник по машинам опорных векторов

Наконец, есть много сообщений на сайтах вопросов и ответов, в которых запрашиваются простые объяснения SVM, ниже приведены два варианта, которые могут оказаться полезными.

  • Что означает машина опорных векторов (SVM) с точки зрения непрофессионала?
  • Пожалуйста, объясните, что такое машины опорных векторов (SVM), как будто я пятилетний ребенок

Резюме

В этом посте вы узнали об алгоритме опорных векторов для машинного обучения. Вы узнали о:

  • Классификатор максимальной маржи, который предоставляет простую теоретическую модель для понимания SVM.
  •  Классификатор мягкого поля, который является модификацией классификатора максимального поля, чтобы ослабить поле для обработки зашумленных границ классов в реальных данных.
  • Машины опорных векторов и как можно переформулировать алгоритм обучения в виде ядра скалярного произведения, а также как можно использовать другие ядра, такие как полиномиальное и радиальное.
  • Как можно использовать числовую оптимизацию для изучения гиперплоскости и что в эффективных реализациях используется альтернативная схема оптимизации, называемая последовательной минимальной оптимизацией.

У вас есть вопросы о SVM или об этом сообщении?
Спрашивайте в комментариях и я постараюсь ответить.

Узнайте, как работают алгоритмы машинного обучения!

Посмотрите, как работают алгоритмы в минутах

…только с арифметикой и простыми примерами

Узнайте, как это делается в моей новой электронной книге:
Алгоритмы главного машинного обучения

Это охватывает Объяснения и Примеры из 10 верхних алгоритмов , например:
Линеарная регрессия , K-nearest соседки , .

Наконец, отодвиньте занавес на

Алгоритмы машинного обучения

Пропустите академические предметы. Просто Результаты.

Посмотреть, что внутри

О Джейсоне Браунли

Джейсон Браунли, доктор философии, специалист по машинному обучению, который обучает разработчиков тому, как получать результаты с помощью современных методов машинного обучения с помощью практических руководств.

Просмотреть все сообщения Джейсона Браунли →

Изучение векторного квантования для машинного обучения

Алгоритмы бэггинга и ансамбля случайного леса для машинного обучения

Вопрос времени: более быстрый анализ перколятора с помощью эффективного обучения SVM для крупномасштабной протеомики

  • Список журналов
  • Рукописи авторов HHS
  • PMC6420878

J Протеом Рез. Авторская рукопись; доступно в PMC 2019 4 мая.

Опубликовано в окончательной редакции как:

J Proteome Res. 2018 4 мая; 17(5): 1978–1982.

Published online 2018 Apr 6. doi: 10.1021/acs.jproteome.7b00767

PMCID: PMC6420878

NIHMSID: NIHMS1014248

PMID: 29607643

† and ‡

Author information Copyright and License information Disclaimer

Дополнительные материалы

Перколятор — важный инструмент для значительного улучшения результатов поиска в базе данных и последующего последующего анализа. Используя машины опорных векторов (SVM), Percolator повторно калибрует совпадения пептидного спектра (PSM) на основе изученной границы решения между целями и ловушками. Чтобы сократить время анализа крупномасштабных наборов данных, мы обновляем механизм обучения Percolator SVM с помощью программных и алгоритмических оптимизаций, а не эвристических подходов, которые требуют тщательного изучения их влияния на изученные параметры в различных настройках поиска и наборах данных. Мы показываем, что, оптимизировав исходный алгоритм обучения Percolator, l 2 -SVM-MFN, для крупномасштабного обучения SVM требуется почти только треть исходного времени выполнения. Кроме того, мы показываем, что благодаря использованию широко используемого алгоритма Trust Region Newton (TRON) вместо l 2 -SVM-MFN крупномасштабное обучение Percolator SVM сокращается почти до одной пятой исходного времени выполнения. . Важно отметить, что эти ускорения влияют только на скорость, с которой Percolator сходится к глобальному решению, и не влияют на производительность повторной калибровки. Обе обновленные версии l 2 -SVM-MFN и TRON оптимизированы в кодовой базе Percolator для многопоточного и однопоточного использования и доступны по лицензии Apache на bitbucket.org/jthalloran/percolator_upgrade.

Ключевые слова: тандемная масс-спектрометрия, машинное обучение, метод опорных векторов, перколятор, TRON

Первоначально выпущенный десять лет назад, перколятор 1 стал неотъемлемым инструментом во многих конвейерах тандемной масс-спектрометрии (МС/МС) для точный постобработочный анализ поиска в базе данных. Эта растущая известность во многом обязана постоянному развитию Percolator 2,3 и его синергия со многими популярными поисковыми системами. 4–8 Недавняя работа с крупномасштабными наборами данных была сосредоточена на ускорении времени выполнения Percolator путем обучения на меньших случайно выбранных наборах PSM (так называемая субдискретизация 3 ) для аппроксимации крупномасштабных параметров SVM. В этом приближенном подходе размер случайной выборки, используемой для обучения, выбирается по усмотрению пользователя без каких-либо общих гарантий. Однако выбор этого определяемого пользователем параметра может быть в целом неочевидным, учитывая лежащий в основе Percolator метод машинного обучения (т. Е. Случайное удаление многих точек данных, которые могут включать опорные векторы аппроксимируемой границы решения SVM, потенциально изменяет качество аппроксимированных параметров; см. дополнительный рисунок S-1) и очень изменчивый характер данных МС/МС (т. е. наборы данных и идентифицированные PSM значительно различаются в зависимости от размеров набора данных, типов машин, параметров поиска, организмов, переваривающих ферментов и т. д.). Вместо того, чтобы сосредоточиться на приближенном подходе, мы вместо этого исследуем ускорение времени выполнения Percolator за счет алгоритмических и программных улучшений его механизма обучения SVM. Поскольку такие улучшения обычно ускоряют время обучения перколятора, не влияя на качество изученных параметров, работа, описанная здесь, также дополняет будущие усилия, в которых используется субдискретизация (или аналогичный приблизительный подход).

В этой работе мы исследуем два неэвристических ускорения постобработки Percolator: обширная оптимизация текущего модуля обучения SVM, l 2 -SVM-MFN, 9 и использование более нового, современного -современный алгоритм обучения SVM, который минимизирует ту же целевую функцию, Trust Region Newton (TRON), 10,11 , широко используемый для крупномасштабных задач машинного обучения. Здесь мы ссылаемся на встроенный SVM-решатель Percolator как l 9.0332 2 -SVM-MFN, наша оптимизированная версия SVM-решателя Percolator как l 2 -SVM-MFN*, и наша реализация алгоритма Trust Region Newton, оптимизированная для использования в Percolator как TRON. l 2 -SVM-MFN* и TRON сокращают время обучения перколятора в готовом крупномасштабном SVM в среднем до 65,19% и 79,37% соответственно по сравнению крупномасштабные наборы данных для многопоточных сред. Для сред, ограниченных одним потоком, специализированные реализации l 2 -SVM-MFN* и TRON сокращают время обучения крупномасштабного перколятора в среднем на 60,65 % и 69,95 % соответственно на крупномасштабных наборах данных. Все оптимизации были написаны в Percolator (версия 3.01, загружена 31 мая 2017 г.) без каких-либо зависимостей от внешних пакетов. Полученное программное обеспечение свободно доступно как программное обеспечение с открытым исходным кодом под исходной лицензией Percolator на bitbucket.org/jthalloran/percolator_upgrade.

Обучение SVM в Percolator

В качестве входных данных Percolator получает PSM цели и приманки для алгоритма поиска в базе данных (например, Sequest, 12 MS-GF+, 13 X!Tandem, 14 или DRIP 8,15 ) вместе с функциями подробное описание каждого PSM, вычисленного во время поиска (например, оценка, масса пептида, отклонение массы от массы предшественника наблюдаемого спектра и т. д.). Затем используется трехкратная перекрестная проверка 2 (наряду с дополнительной перекрестной проверкой, вложенной в каждую внешнюю складку) для оценки высококачественных обучающих PSM с использованием целевой-приманки q -значения 16,17 и обучить дискриминационный классификатор. Обученный дискриминационный классификатор представляет собой линейный SVM, в котором вычисляется гиперплоскость, которая максимизирует мягкую маржу между обучающими PSM цели и приманки. Обратите внимание, что параметры, полученные в SVM, определяются исключительно опорными векторами, то есть точками данных, лежащими на границе изученной границы решения.

Формулировка SVM с мягким запасом является выпуклой, поэтому гарантируется глобальное решение. Формула SVM Percolator включает l 2 член регуляризации, сохраняющий выпуклость и улучшающий обобщение невидимых данных. SVM хорошо подходят для классификации целевых и ложных PSM, поскольку они надежны и могут быть быстро обучены для линейного SVM, такого как Percolator. После завершения перекрестной проверки изученные гиперплоскости затем объединяются, чтобы сформировать окончательную границу решения Percolator, и используются для повторной оценки PSM для улучшения калибровки. В настоящее время Percolator поддерживает многопоточность (с использованием OpenMP) для перекрестной проверки, при этом одна SVM обучается для каждого потока внутри гнезда.

Решатель SVM

Хотя общий выпуклый метод (т. е. градиентный спуск, сопряженный градиентный спуск, метод Ньютона или L-BFGS) может использоваться для решения формулы SVM Percolator, сообщество машинного обучения разработало высокоэффективные алгоритмы для Обучение СВМ. Во время его первоначального выпуска в Ref. 1, алгоритм обучения SVM Percolator ( l 2 -SVM-MFN 9 ) считался современным и особенно эффективным для крупномасштабных задач. Впоследствии Trust Region Newton (TRON) 10 был введен для решения одной и той же задачи SVM и показал быструю сходимость на различных наборах данных. 18 TRON — это алгоритм второго порядка, в котором область вокруг текущего решения, называемая областью доверия , корректируется на основе аппроксимированного уменьшения целевой функции. Затем вычисляется усеченный шаг Ньютона в пределах области доверия, который используется для обновления объективных весов, и весь процесс повторяется до сходимости. TRON остается современным и широко используется, а в недавней работе исследуются практические улучшения алгоритма. 19,20

Сведения о программном обеспечении

Оптимизированная версия Percolator доступна для бесплатной загрузки на основе Percolator версии 3.01 (загружена 31 мая 2017 г.). Реализация Percolator l 2 -SVM-MFN, происходящая из реализации C++ SVM lin , 21 , была оптимизирована за счет сочетания обширной реструктуризации кода, использования низкоуровневых функций линейной алгебры и использование многопоточности в критических, узких местах вычислений (результаты разработки более подробно обсуждаются в разделе «Результаты»). TRON, основанный на реализации C из LIBLINEAR 11 (версия 2.11, загружена 24 апреля 2017 г.) также был оптимизирован для использования в кодовой базе Percolator.

Для многопоточных вычислительных сред вычисления распределяются между заданным пользователем числом потоков ЦП с помощью параметра -nr NUMTHREADS, где NUMTHREADS по умолчанию равно максимальному количеству системных потоков, если указанное значение превышает максимальное. Для вычислительных сред, где многопоточность невозможна, l 2 -SVM-MFN* и TRON специально оптимизированы для использования одного потока; для каждой оценки целевой функции в рамках итерации выполняется одно низкоуровневое умножение матрицы на вектор, чтобы быстро оценить параметры (т. е. изученную гиперплоскость), рассчитанные на предыдущей итерации. Реализация с одним потоком требует немного больше памяти, чем обычный Percolator, для правильного форматирования матрицы данных для низкоуровневого вызова произведения матрицы-вектора, хотя на практике это незначительно (например, накладные расходы памяти составляли ~ 1,6% стандартного использования памяти Percolator, или 90 МБ для набора данных Wu).

Наборы данных

Все пин-файлы Percolator, используемые в этой работе (как крупномасштабные, так и данные разработки), доступны для загрузки на сайте jthalloran.ucdavis.edu.

Крупномасштабные наборы данных

Наши два крупномасштабных эталонных набора основаны на двух наборах данных (т. е. наборе данных Кима 22 и наборе данных Ву 23 ) и параметрах поиска, используемых для сравнения результатов синхронизации в Ref. 3. Данные Kim были получены из 17 тканей взрослого организма, семи тканей плода и шести типов гемопоэтических клеток, собранных с использованием LTQ Orbitrap Velos и Elite, оснащенных системами ВЭЖХ Easy-nLC II nanoflow. Набор данных Wu, созданный в ходе исследования изменения содержания белка в организме человека, состоит из спектров, полученных из 51 лизата лимфобластоидных клеточных линий, где пептиды были помечены TMT 6-plex, и собраны с использованием LTQ Orbitrap Velos. Все спектры были найдены с помощью Tide 7 с использованием Crux версии 3.1 (загружено 21 июня 2017 г.). Чтобы варьировать методы создания ложных целей, базы данных ложных целей Кима и Ву были созданы путем обращения пептидов и перетасовки, соответственно, с использованием индекса Tide. 4 459 463 спектра набора данных Wu были найдены в базе данных IPI Human ver. 3.74 (источник, дата обращения: 22 мая 2014 г.) с использованием триптического расщепления, допуск массы фрагмента Tide по умолчанию, окно массы предшественника ±10 ppm, до двух пропущенных расщеплений, окисление метионина и мечение TMT N-концевых аминокислот, в результате было создано 8 313 602 целевых и ложных PSM. 4 084 132 спектра набора данных Кима были сопоставлены с базами данных человека Swiss-Prot и Swiss-Prot+TrEMBL (источник, дата обращения: 24 июля 2017 г.), объединенными с базой данных распространенных загрязняющих веществ (источник, дата обращения: 24 июля 2017 г.) с использованием полутриптическое расщепление, допуск по массе фрагментов Tide по умолчанию, ± Окно допуска массы предшественника 10 ppm, до двух пропущенных расщеплений, до двух окислений метионина на пептид и переменное ацетилирование N-концов, что приводит к 7 710 057 целевых и ложных PSM.

Наборы данных для разработки

Во время разработки два небольших набора данных использовались для отладки и отображения относительного улучшения последовательных оптимизаций. Первый, который мы называем «Дрожжи», состоит из 35 467 спектров Saccharomyces cerevisiae , собранных с использованием триптического расщепления с последующим получением с использованием сканирования предшественников с низким разрешением и фрагментов ионов с низким разрешением (более подробно описано в ссылке 1). Второй, который мы называем плазмодием, состоит из 12,594 спектра, полученные из образца Plasmodium falciparum , расщепленного с использованием Lys-C и помеченного изобарическим агентом для повторной маркировки ТМТ, собранные с использованием сканирования предшественников с высоким разрешением и фрагментных ионов с высоким разрешением (более подробно описано в ссылке 24).

Пептиды-приманки были созданы путем перетасовки целевых пептидов. Plasmodium искали с использованием Tide с окном массы предшественника ± 50 ppm, Lys-C, фиксированным карбамидометилированием и фиксированным TMT-мечением лизина и N-концевых аминокислот, что дало 23,922 целевые и ложные ПСМ. Поиск дрожжей проводился с использованием Tide с массовым окном предшественника Томсона ±3, трипсином без подавления пролина, отсутствием пропущенных расщеплений и фиксированным карбамидометилированием, в результате чего было получено 140 346 целевых и ложных PSM. Для дальнейшего стресс-тестирования алгоритмов во время разработки семнадцать внутренних функций, подробно описывающих каждый PSM, были добавлены в пин-файлы Yeast and Malaria, выводимые Tide. Значения XCorr p также были рассчитаны с использованием Tide для набора данных MS2 Yeast с низким разрешением и добавлены к соответствующему файлу контактов.

Экспериментальная среда

Все эксперименты Percolator проводились с использованием многоядерного вычислительного сервера с одним терабайтом оперативной памяти, состоящего из процессоров Intel Xeon E7–4830 v3 с тактовой частотой 2,10 ГГц. Для всех временных тестов многопоточность в процедуре перекрестной проверки Percolator была отключена, чтобы уменьшить дополнительные накладные расходы на планирование и точно измерить скорость различных алгоритмов обучения SVM.

Разработка

Прогресс оптимизации был отмечен несколькими основными этапами разработки:

  1. Начальный — успешная реализация алгоритма обучения в рамках SVM-фреймворка Percolator. Это относится к TRON, хотя l 2 -SVM-MFN также проиллюстрирован для этой стадии для полноты картины.

    Открыть в отдельном окне

    Процент исходного времени выполнения обучения Percolator SVM для наборов данных разработки после каждого набора основных l 2 -SVM-MFN* и ускорений TRON. Обучение SVM с использованием оригинала l 2 -SVM-MFN потребовалось 174,6 секунды и 27,2 секунды для наборов данных Yeast и Plasmodium соответственно.

  2. Реструктурированный — реструктуризация и упрощение кода. Этот этап был направлен на оптимизацию кода алгоритма обучения SVM. l 2 -SVM-MFN* больше всего выиграл от этого, так как большие части кода были значительно реструктурированы и сжаты.

  3. низкоуровневый — многие операции были оптимизированы с использованием низкоуровневых функций линейной алгебры (это значительно сократило время выполнения TRON из-за плотного, а не разреженного представления функций в Percolator).

  4. однопоточный — алгоритм обучения SVM был оптимизирован для использования с одним потоком (оценки целевой функции как в TRON, так и в l 2 -SVM-MFN* были оптимизированы с использованием низкоуровневой матрицы -вектор умножить).

  5. nr-k — многопоточность с потоками k . Для обоих алгоритмов обучения умножение матрицы на вектор в однопоточной оптимизации вместо этого распараллеливается. Для TRON это включает распараллеливание оценки Гессиана и вычисление градиента (более подробно обсуждается в [25]). Для l 2 -SVM-MFN*, эта новая работа включала распараллеливание основных вычислительных узких мест в процедурах сопряженного градиента и линейного поиска.

Сравнительное время выполнения наборов данных разработки после каждого этапа показано на . Ожидалось, что многопоточность окажет значительное влияние на крупномасштабные эксперименты, но не ожидалось, что она улучшит высокооптимизированную однопоточную реализацию наборов данных для разработки из-за их небольшого размера (как оказалось в случае с 9).0044 l 2 -SVM-MFN*, где однопоточная оптимизированная реализация показала лучшие результаты на наборах разработчиков, а многопоточность оказалась гораздо более эффективной в крупномасштабной среде выполнения). Однако благодаря эффективности алгоритма и его упрощенному дизайну TRON с несколькими потоками оказался чрезвычайно быстрым даже на таких небольших наборах данных, значительно превзойдя своего однопоточного оптимизированного аналога. Отметим, что из-за зависимости l 2 -SVM-MFN от эвристики относительной остановки для досрочного завершения алгоритма параметры, полученные с использованием TRON, могут немного отличаться. Однако существенной разницы в производительности не наблюдалось из-за незначительной разницы в изученных параметрах (рисунки и ).

Открыть в отдельном окне

Точность постобработки перколятора по наборам для разработки с использованием различных алгоритмов обучения SVM. На графике представлены значения q в зависимости от количества значимых PSM после повторной калибровки Percolator PSM цели и ложной цели с использованием алгоритмов l 2 -SVM-MFN, l 2 -SVM-MFN* и TRON.

Открыть в отдельном окне

Точность постобработки перколятора для крупномасштабных эталонных наборов данных. Нанесены q -значения в зависимости от количества значимых PSM после повторной калибровки перколятором PSM цели и ловушки с использованием алгоритмов l 2 -SVM-MFN, l 2 -SVM-MFN* и TRON.

Попытка дальнейшего повышения скорости путем смешивания однопоточной оптимизации с многопоточной не привела к улучшению времени выполнения и запутала кодовую базу.

Крупномасштабные результаты синхронизации

Время выполнения представлено как отношение TRON или l 2 -SVM-MFN* Время выполнения, деленное на время выполнения исходного l 2 -SVM-MFN Реализация перколятора. Время работы всех перколяторов (с использованием l 2- SVM-MFN, l 2 -SVM-MFN* и алгоритмов обучения TRON) усреднялось по десяти запускам, всего было проведено 620 тестов синхронизации. Ускорение Percolator, обеспечиваемое использованием l 2 -SVM-MFN* и TRON с несколькими потоками, было протестировано с использованием -nr, установленного на 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 50 и 60 (показаны синим цветом на рис.). Когда для -nr установлено значение 1, однопоточные оптимизированные версии TRON и l 2 -SVM-MFN* используются (на графике красным цветом). Во всех отчетах о времени выполнения оценивалось только время обучения SVM, измеряемое как время, прошедшее от начала обучения до его окончания.

Открыть в отдельном окне

Время работы перколятора с использованием l 2 -SVM-MFN* и TRON по сравнению с исходной реализацией l 2 -SVM-MFN. Ось y обозначает время работы Percolator с использованием l 2 -SVM-MFN* (красный график) и TRON (синий график), деленное на время работы Percolator с использованием л 2 -SVM-MFN. Ось x обозначает количество потоков, используемых для многопоточности l 2 -SVM-MFN* (сплошная красная кривая) и многопоточности TRON (сплошная синяя кривая). Время работы l 2 -SVM-MFN* и TRON, оптимизированных для одного потока, показано красным и синим пунктиром соответственно. Все заявленные времена поиска представляют собой среднее значение десяти запусков (среднее время работы перколятора l 2 -SVM-MFN составило 2,94 часа и 3,89 часа для наборов данных Kim и Wu соответственно).

TRON и l 2 -SVM-MFN* улучшают время работы перколятора для крупномасштабного анализа во всех экспериментах. l 2 -SVM-MFN*, оптимизированный для однопоточной обработки, сокращает время работы Percolator на 55,91 % и 65,38 % (ускорение в 2,27 и 2,89 раза) для наборов данных Kim и Wu соответственно. l 2 -SVM-MFN* с многопоточностью сократил время выполнения Percolator на 60,21 % и 70,17 % (ускорение в 2,51 и 3,35 раза) для наборов данных Kim и Wu соответственно. Однопоточная оптимизированная реализация TRON сокращает время выполнения Percolator на 71,31% и 68,59.% (ускорение в 3,49 и 3,18 раза) для наборов данных Kim и Wu соответственно. Для многопоточных сред TRON сокращает время выполнения Percolator на 77,46% и 81,28% (ускорение в 4,44 и 5,34 раза) для наборов данных Kim и Wu соответственно. Это экономит часы работы Percolator почти во всех случаях (TRON с номером ≥ 10 завершился менее чем за час для обоих наборов данных) без какого-либо ухудшения производительности повторной калибровки.

Мы показали, что время выполнения Percolator может быть значительно улучшено за счет алгоритмического ускорения его текущего алгоритма обучения SVM, л 2 -SVM-MFN. Кроме того, время выполнения Percolator можно еще больше улучшить с помощью современного алгоритма обучения TRON. При крупномасштабном анализе эти ускорения экономят несколько часов времени анализа как для многопоточных, так и для однопоточных вычислительных сред. Важно отметить, что, поскольку эти улучшения являются оптимизацией алгоритмов и программного обеспечения, они не ставят под угрозу изученные параметры (и последующую производительность повторной калибровки) и дополняют будущий анализ и использование приблизительных методов, таких как субдискретизация.

Дополнительный файл

Нажмите здесь для просмотра. (134K, pdf)

Эта работа была поддержана Национальным центром развития трансляционных наук (NCATS), Национальным институтом здравоохранения, посредством гранта UL1 TR001860.

Вспомогательная информация

Различия в количестве значимых PSM при q = 0,01 между решением точной крупномасштабной задачи (с использованием оригинального решателя Percolator, L2-SVM-MFN) и несколькими приближенными решениями, найденными с использованием понижающей дискретизации (дополнительный Рисунок S–1).

(1) Калл Л; Кентербери Дж.; Уэстон Дж.; Благородный ВС; МакКосс МДж
Метод полуконтролируемого машинного обучения для идентификации пептидов из наборов данных протеомики дробовика. Нац. Методы
2007, 4, 923–25. [PubMed] [Google Scholar]

(2) Гранхольм В.; Благородный ВС; Колл Л
Схема перекрестной проверки алгоритмов машинного обучения в протеомике дробовика. Биоинформатика BMC
2012, 13, С3. [Бесплатная статья PMC] [PubMed] [Google Scholar]

(3) Мэтью Т.; Маккос МДж; Благородный ВС; Келл Л
Быстрая и точная частота ложных обнаружений белков в крупномасштабных наборах данных протеомики с помощью перколятора 3.0. Журнал Американского общества масс-спектрометрии
2016, 27, 1719–1727. [Бесплатная статья PMC] [PubMed] [Google Scholar]

(4) Brosch M; Ю Л; Хаббард Т; Чоудхари Дж.
Точная и чувствительная идентификация пептидов с помощью Mascot Percolator. J. Протеом Рез
2009, 8, 3176–3181. [Бесплатная статья PMC] [PubMed] [Google Scholar]

(5) Гранхольм В.; Ким С; Наварро Дж.К.; Сьолунд Э; Смит Р.Д.; Колл Л
Быстрый и точный поиск в базе данных с помощью MS-GF+ Percolator. J. Протеом Рез
2013, 890–897. [Бесплатная статья PMC] [PubMed] [Google Scholar]

(6) Xu M; Ли З; Ли Л
Сочетание перколятора с X! Тандем для точной и чувствительной идентификации пептидов. Журнал исследований протеома
2013, 12, 3026–3033. [PubMed] [Академия Google]

(7) МакИлвейн С; Тамура К; Кертес-Фаркаш А; Грант СЕ; диаметр В; Фрюэн ​​Б; Хоуберт Дж.Дж.; Хоопманн М.Р.; Колл Л; англ Дж.К.; Маккос МДж; Благородный ВС
Суть: быстрый тандемный масс-спектрометрический анализ белков с открытым исходным кодом. J. Протеом Рез
2014, 13, 4488–4491. [Бесплатная статья PMC] [PubMed] [Google Scholar]

(8) Halloran JT; Билмес Дж. А.; Благородный ВС
Динамическая байесовская сеть для точного обнаружения пептидов из тандемных масс-спектров. Журнал исследований протеома
2016, 15, 2749–2759. [Бесплатная статья PMC] [PubMed] [Google Scholar]

(9) Кирти СС; ДеКосте Д
Модифицированный конечный метод Ньютона для быстрого решения крупномасштабных линейных SVM. Журнал исследований машинного обучения
2005, 6, 341–361. [Google Scholar]

(10) Лин Си-Джей; Венг Р.К.; Кирти СС
Доверяйте ньютоновским методам области для крупномасштабной логистической регрессии. Материалы 24-й международной конференции по машинному обучению. 2007 г.; стр. 561–568. [Google Scholar]

(11) Fan R-E; Чанг К.В.; Се CJ; Ван Х-Р; Лин Си-Джей
LIBLINEAR: библиотека для большой линейной классификации. Журнал исследований машинного обучения
2008, 9, 1871–1874 гг. [Google Scholar]

(12) англ JK; Маккормак А.Л.; Йейтс младший III
Подход к корреляции тандемных масс-спектральных данных пептидов с последовательностями аминокислот в базе данных белков. 1994, 5, 976–989. [PubMed] [Google Scholar]

(13) Ким С; Певзнер П.А.
MS-GF+ делает успехи в создании универсального инструмента поиска в базе данных для протеомики. 2014, 5, 5277. [Бесплатная статья PMC] [PubMed] [Google Scholar]

(14) Craig R; Бивис RC
ТАНДЕМ: сопоставление белков с тандемными масс-спектрами. Биоинформатика
2004, 20, 1466–1467. [PubMed] [Академия Google]

(15) Халлоран Дж. Т.; Рок ДМ
Градиенты генеративных моделей для улучшенного дискриминационного анализа тандемных масс-спектров. Достижения в области нейронных систем обработки информации. 2017; стр. 5728–5737. [Google Scholar]

(16) Этаж JD
Прямой подход к частоте ложных открытий. Дж. Р. Стат. Соц
2002, 64, 479–498. [Google Scholar]

(17) Keich U; Кертес-Фаркаш А; Благородный ВС
Улучшенная процедура оценки частоты ложных открытий для протеомики дробовика. J. Протеом Рез
2015, 14, 3148–3161. [Бесплатная статья PMC] [PubMed] [Google Scholar]

(18) Лин С.-Дж.; Венг Р.К.; Кирти СС
Метод Ньютона области доверия для крупномасштабной логистической регрессии. Журнал исследований машинного обучения
2008, 9, 627–650. [Google Scholar]

(19) Lee M-C; Чан WL; Лин Си-Джей
Быстрое умножение матрицы на вектор для крупномасштабной логистической регрессии в системах с общей памятью. Интеллектуальный анализ данных (ICDM), Международная конференция IEEE 2015 года. 2015 г.; стр. 835–840. [Google Scholar]

(20) Hsia C-Y; Чжу Ю; Лин Си-Джей
Исследование правил обновления области доверия в методах Ньютона для крупномасштабной линейной классификации. Азиатская конференция по машинному обучению. 2017; стр. 33–48. [Академия Google]

(21) Синдхвани В.; Кирти СС
Методы Ньютона для быстрого решения линейных SVM с полууправлением. Крупномасштабные машины с ядром
2007, 155–174. [Google Scholar]

(22) Ким М. С.; Пинто СМ; Гетнет Д; Ниружоги Р.С.; Манда СС; Черкадий Р; Мадугунду А.К.; Келкар Д.С.; Иссерлин Р.; Джейн С
Черновая карта протеома человека. Природа
2014, 509, 575. [Бесплатная статья PMC] [PubMed] [Google Scholar]

(23) Wu L; Кандиль С.