Сзв м как заполнять: Страница не найдена \ КонсультантПлюс

Содержание

СЗВ-М — образец заполнения в 2020 году

Чтобы Пенсионный фонд принял отчет СЗВ-М с первого раза, в нем должны быть указаны корректные данные о работодателе и застрахованных лицах. Кроме того, заполненная форма должна своевременно попасть в ПФР допустимым способом, зависящим от численности застрахованных лиц. Можно ли в 2022 году заполнить СЗВ-М онлайн бесплатно, где взять бланк, из каких разделов он состоит и какие данные нужны для заполнения, узнайте из нашего материала. Здесь же вы найдете образец заполнения СЗВ-М в 2022 году по новой форме, а также ответы на другие сопутствующие вопросы.

Кто обязан сдавать отчет СЗВ-М

Кто из работодателей обязан представлять СЗВ-М, поможет разобраться информация на рисунке:

Принимая решение, нужно ли представлять в ПФР форму СЗВ-М, учитывайте следующее:

  • Отсутствие в отчетном периоде начислений и выплат по тем или иным договорам не является основанием для непредставления СЗВ-М. Данные о физлицах, с которыми заключены такие договоры, включаются в отчет.

  • Отсутствие сотрудников в штате и физлиц, с которыми заключены договоры ГПХ, при наличии у компании директора — единственного учредителя, по мнению ПФР, не повод не представлять СЗВ-М.

Вопрос о том, нужно ли представлять СЗВ-М на руководителя — единственного учредителя, вызывает много споров и судебных разбирательств. Однако чиновники требуют в такой ситуации отчитываться по форме СЗВ-М (письма Минтруда от 16.03.2018 № 17-4/10/В-1846, от 29.03.2018 № ЛЧ-08-24/5721), а судьи их поддерживают (постановление АС Центрального округа от 18.04.2019 по делу № А14-1839/2018).

Ранее мы рассказывали, какие законодательные нормы обязывают представлять СЗВ-М на единственного учредителя.

Нужно ли заполнять СЗВ-М на совместителей и декретниц, разъяснили эксперты КонсультантПлюс. Получите пробный доступ к К+ бесплатно и переходите в Готовое решение.

Где взять бланк и когда представить готовый СЗВ-М в ПФР

С 30.05.2021 (то есть с отчета за май 2021) форма СЗВ-М и порядок ее заполнения утверждены постановлением Правления ПФР от 15. 04.2021 № 103п. Она представляет собой один из отчетов работодателей в Пенсионный фонд, содержащий персонифицированные сведения о физлицах (Ф.И.О., СНИЛС и ИНН) — сотрудниках, с которыми оформлены трудовые договоры, и лицах, заключивших договоры гражданско-правового характера (ГПХ). Скачать форму можно бесплатно, кликнув по картинке ниже:

Бланк СЗВ-М

Скачать

СЗВ-М необходимо представлять ежемесячно — не позднее 15-го числа месяца, следующего за отчетным (п. 2.2 ст. 11 закона «Об индивидуальном (персонифицированном) учете в системе обязательного пенсионного страхования» от 01.04.1996 № 27-ФЗ).

В отдельных случаях на заполнение СЗВ-М можно потратить чуть больше указанного времени: если 15-е число выпадает на выходной или праздничный день, крайний отчетный срок сдвигается на первый рабочий день (письмо ПФР от 07.04.2016 № 09-19/4844).

Какой штраф за нарушения с СЗВ-М, узнайте в Готовом решении от КонсультантПлюс. Пробный доступ к системе можно получить бесплатно.

Далее расскажем о составе отчетной формы и покажем, как выглядит образец СЗВ-М.

Четыре информационных блока для заполнения

Структура и состав данных СЗВ-М довольно просты. Если у работодателя не много застрахованных лиц, весь отчет может поместиться на 1 странице.

Всего в отчете 4 раздела:

  1. Данные о работодателе.

Регистрационный номер в ПФР — это 12-значный цифровой код, присваиваемый каждому работодателю при регистрации в Пенсионном фонде. Чтобы убедиться, что имеющиеся у составителя отчета данные об этом номере достоверны, можно его проверить на сайте ФНС, открыв выписку из ЕГРЮЛ/ЕГРИП. В выписке регистрационный номер указан в разделе «Сведения о страхователе в Пенсионном фонде».

Остальные сведения о работодателе, вносимые в форму, должны быть полностью идентичными данным из учредительных документов (в части наименования компании), а также Свидетельства о постановке на учет в налоговом органе (данные об ИНН и КПП).

  1. Отчетный период.

В этом разделе нужно проставить всего 2 цифры: календарный год и номер отчетного месяца в установленном формате.

  1. Тип формы.

В этом разделе указывается один из трех предлагаемых типов формы: «Исходная», «Дополняющая» или «Отменяющая». Расшифровка каждого типа приведена в п. 13 Порядка заполнения.

По информации из этого раздела специалисты ПФР поймут, сдаете ли вы отчет СЗВ-М с исходными данными за отчетный период или корректируете уже поданную форму при выявлении в ней недостающих или ошибочных данных.

  1. Сведения о застрахованных лицах.

Для заполнения раздела нужны корректные данные о Ф.И.О., СНИЛС и ИНН застрахованных лиц.

При этом в графе «Фамилия, имя, отчество» отчество заполняется при его наличии. Это же правило касается графы «ИНН» — если у физлица его нет, данная графа не заполняется. А вот без данных о СНИЛС отчет сдать не получится.

Завершается оформление отчета стандартной процедурой — подписанием ответственным лицом с проставлением его должности и расшифровкой Ф. И.О. Печатью отчет заверяется только при ее наличии у работодателя.

Посмотреть и скачать образец СЗВ-М 2022 года по новой форме можно в КонсультантПлюс, получив бесплатный пробный доступ:

Скачайте наш чек-лист по заполнению СЗВ-М и не допускайте ошибок.

Читайте также еще об одном новом отчете в ПФР, который нужно сдавать вместе с СЗВ-М.

Бесплатная программа по формированию отчета

Работодатели, сдающие отчетность в ПФР впервые, часто интересуются, можно ли заполнить СЗВ-М онлайн и есть ли бесплатные сервисы формирования этой формы.

Существует немало платных и бесплатных сервисов по формированию отчетных форм для ПФР. К примеру, для заполнения СЗВ-М онлайн бесплатно можно воспользоваться предложением от ПФР. На его официальном сайте можно скачать программу Spu_orb и сформировать набор документов для Пенсионного фонда, в том числе СЗВ-М. Эта программа распространяется бесплатно.

Устанавливается программа быстро и не требует специальных компьютерных навыков.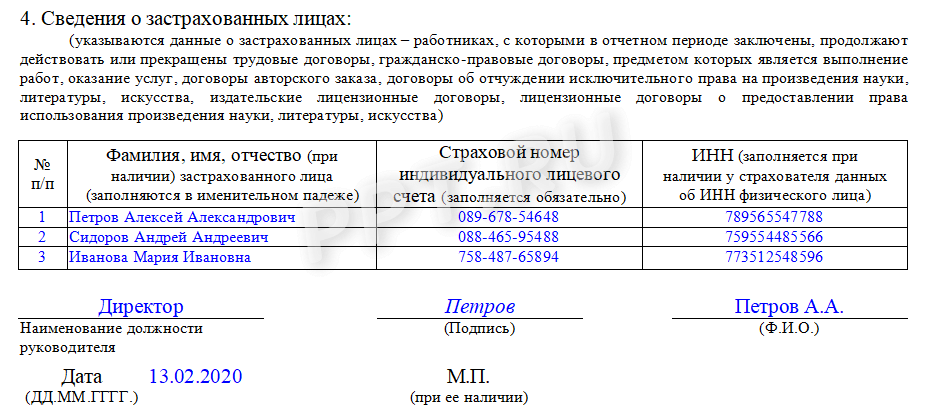 Достаточно следовать подсказкам мастера установки:

Познакомьтесь с нашими материалами о том, как современные технологии облегчают формирование разнообразных учетных и отчетных документов:

  • «Онлайн-заполнение товарной накладной: какие есть сервисы»;

  • «Сервисы для заполнения справки 2-НДФЛ онлайн»;

  • «Обзор программ и сервисов для ведения бухгалтерии онлайн».

Как заполнить отчетную форму в программе ПФР

Рассмотрим, как заполнять отчет СЗВ-М после установки и запуска программы Spu_orb.

Основные этапы оформления отчета:

  1. Ввод данных о работодателе.

Для начала работы в меню «Настройки» следует выбрать пункт «Реквизиты предприятия» и отразить необходимую информацию:

  1. Ввод данных о сотрудниках.

Чтобы заполнить СЗВ-М данными о сотрудниках, в меню «Ввод данных» выберите отчетную форму «Сведения о застрахованных лицах: СЗВ-М».

Затем укажите отчетные месяц и год, тип формы (исходная) и дату заполнения формы с помощью кнопки «Добавить» и введите данные о сотрудниках:

Если вы ошиблись при вводе данных, программа на это укажет:

В отчет включаются работники, с которыми в отчетном месяце действовал трудовой договор или договор подряда — хотя бы один день. Тот факт, перечислял работодатель по таким контрактам вознаграждения или нет, значения не имеет.

После того как данные обо всех сотрудниках внесены в форму, готовый СЗВ-М можно просмотреть с помощью кнопки «Печать», выгрузить и/или распечатать.

Возможность заполнить СЗВ-М онлайн бесплатно предоставляют некоторые коммерческие сайты. Для этого предлагается заполнить необходимыми данными предложенные поля, которые соответствуют содержанию СЗВ-М, и распечатать форму. Однако такие сервисы, как правило, не позволяют проверить корректность введенных данных и сформировать файл для отправки отчета в электронной форме.

В какой форме отчитаться

СЗВ-М можно сдавать на бумаге или электронно в зависимости от числа застрахованных лиц:

С 10.01.2022 если численность застрахованных лиц за прошлый отчетный период 10 и менее человек, работодатель вправе выбрать между бумажным и электронным отчетом. Начиная с 11 работников права выбора нет — в ПФР можно отчитаться только электронно (п.  2 ст. 8 федерального закона от 01.04.1996 № 27-ФЗ).

Прочитайте также о том, можно ли отправить СЗВ-М по почте.

Итоги

Форма СЗВ-М представляется ежемесячно не позднее 15-го числа месяца, следующего за отчетным. В ней указываются данные о работодателе: регистрационный номер в ПФР, наименование, ИНН и КПП, а также корректные сведения о Ф.И.О., СНИЛС и ИНН застрахованных лиц, с которыми в отчетном месяце были заключены, продолжали действовать или прекращены трудовые договоры или договоры ГПХ.

Заполнить СЗВ-М онлайн бесплатно в 2022 году можно на коммерческих интернет-сайтах. Но безопаснее использовать специальную программу от ПФР или применяемые большинством работодателей учетные программы, предоставляющие возможность последующей проверки на корректность введенных данных и формирования файла для отправки отчета в электронной форме.

Источники:

  • федеральный закон от 01.04.1996 № 27-ФЗ (ред. от 01.04.2019) «Об индивидуальном (персонифицированном) учете в системе обязательного пенсионного страхования»
  • постановление Правления ПФР от 01.02.2016 № 83п «Об утверждении формы «Сведения о застрахованных лицах»

Правила заполнения СЗВ-М

Какие правила заполнения СЗВ-М действуют в 2019 году? Наша консультация о том, как правильно внести данные в этот отчет.

Где искать правила

Как ни странно, правила заполнения СЗВ-М не утверждены каким-либо отдельным распоряжением Пенсионного фонда. По факту – они вкраплены в сам образец отчета СЗВ-М. Он принят постановлением Правлением ПФР от 1 февраля 2016 года № 83п.

Скачать актуальный бланк формы СЗВ-М на нашем сайте можно здесь.

На наш взгляд, правила заполнения СЗВ-М в 2019 году не должны претерпеть серьезных изменений, поскольку бумажный бланк и состав сведений остались прежними.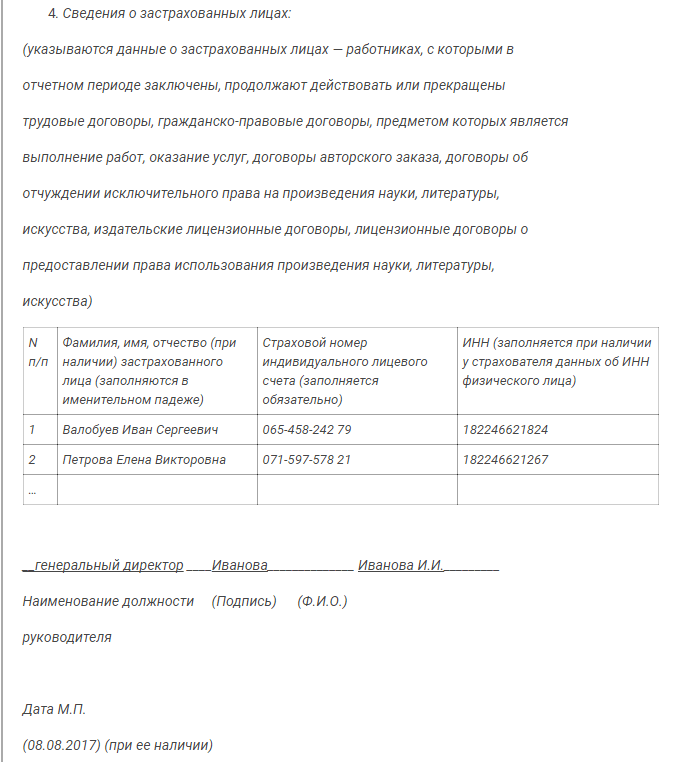

Но как показывает практика, правила заполнения формы СЗВ-М, которые есть в самом бланке, недостаточны для грамотного заполнения исходного отчета. Поэтому обратим ваше внимание на некоторые нюансы.

Особенности

Принципы и правила заполнения СЗВ-М в зависимости от вида и типа организации или ИП отличаются мало. Главное, не забыть указать (см. таблицу):

Для юрлицДля ИП
Точная организационно-правовая форма предприятия согласно уставу и ЕГРЮЛВ графе «Название (краткое)» сделать – «ИП» и Ф.И.О.
Название должности руководителяВ графе о должности – указать, что отчет подписывает именно ИП.
Самого себя включать в 4-й раздел СЗВ-М не нужно, так как сам с собой ИП трудовой договор не заключает

От соблюдения в 2019 году правил заполнения СЗВ-М будет зависеть, придется ли дополнять или корректировать отчет. Поэтому постарайтесь не забыть не только никого из работников, но и исполнителей, подрядчиков и т. п., с которыми фирма (ИП) имела или вступала в договорные отношения в минувшем отчетном периоде (месяце). Кроме того, оперативно отслеживайте информацию о смене сотрудниками и прочими лицами из СЗВ-М своих фамилии, имени, отчества.

Также см. «СЗВ-М: заполняем сведения о застрахованных лицах».

Обратите также внимание, что правила заполнения СЗВ-М в отношении нулевых отчетов отсутствуют в принципе. Дело в том, что фонду не нужны бланки с пустым незаполненным четвертым разделом – без застрахованных лиц.

Подробнее об этом см. «Нулевая СЗВ-М: нужно ли её сдавать и как заполнить».

Кроме того, можно не заполнять отчет на одного лишь директора. При условиях, что он:

  1. не на договоре;
  2. никаких денег от фирмы не получает.

Хотя ПФР обязан принять СЗВ-М, заполненный даже на такого руководителя. И многие так делают, чтобы не иметь с фондом лишним проблем в будущем.

Ниже показано, как правильно заполнить форму СЗВ-М.

В законе прописали, кого включать в СЗВ-М

До 2017 года непосредственно в форме СЗВ-М раскрывалось, каких именно физических лиц нужно включать в ежемесячный отчет. В отчете было сказано, что нужно указывать данные о застрахованных лицах – работниках, с которыми в отчетном периоде заключены, продолжают действовать или прекращены трудовые договоры, гражданско-правовые договоры, предметом которых является выполнение работ, оказание услуг, договоры авторского заказа, договоры об отчуждении исключительного права на произведения науки, литературы, искусства, издательские лицензионные договоры, лицензионные договоры о предоставлении права использования произведения науки, литературы, искусства.

С 2017 года пояснение о том, сведения о каких застрахованных лицах должны содержаться в отчете определены не бланком, а законодательством. Об этом сказано в пункте 2.2 статьи 11 Федерального закона от 01.04.1996 № 27-ФЗ «Об индивидуальном (персонифицированном) учете в системе обязательного пенсионного страхования». Такой порядок заполнения СЗВ-М продолжает действовать и в 2019 году.

Как уточнять отчет в 2019 году

Уточните форму СЗВ-М, если в первичном отчете (с типом «исходная», код «исхд») ошибки. Есть два варианта – сдать дополняющую форму с признаком «доп» или отменяющую с признаком «отмн».

  • Дополняющую СЗВ-М подайте, если отчитались не обо всех сотрудниках. В отчет с признаком «доп» включите только тех сотрудников, сведения о которых добавляете.
  • Отменяющую форму с признаком «отмн» отправьте, если указали в СЗВ-М за июль, например, уволенного в июне или ранее сотрудника.
  • Ошиблись в ИНН сотрудника? Подайте сразу две формы – с кодом «отмн» и с кодом «доп». В отменяющую перенесите запись с ошибочным ИНН из исходной. В дополняющей – повторите с правильным номером.

Уточненные формы подайте в течение пяти рабочих дней со дня получения уведомления из ПФР (п. 37 Инструкции, утвержденной приказом Минтруда России от 21 декабря 2016 № 766н).

Полное руководство для начинающих

Эта статья была опубликована в рамках блога о науке о данных

 

Введение в метод опорных векторов (SVM)

SVM — это мощный контролируемый алгоритм, который лучше всего работает с небольшими наборами данных, но со сложными. Машина опорных векторов, сокращенно SVM, может использоваться как для задач регрессии, так и для задач классификации, но, как правило, они лучше всего работают в задачах классификации. Они были очень известны в то время, когда они были созданы, в 19 веке.90-х годов, и продолжает оставаться популярным методом высокопроизводительного алгоритма с небольшой настройкой.

Надеюсь, вы уже освоили деревья решений, случайный лес, наивный байесовский метод, метод K-ближайшего соседа и ансамблевое моделирование. Если нет, я бы посоветовал вам уделить несколько минут и прочитать о них.

В этой статье я объясню вам, что такое SVM, как работает SVM, а также математическую интуицию, лежащую в основе этого важного алгоритма машинного обучения.

Содержание

  1. Что такое метод опорных векторов?
  2. Когда использовать логистическую регрессию против SVM?
  3. Типы SVM
  4. Как работает SVM
  5. Математическая интуиция за SVM
  6. Скалярное произведение
  7. Использование скалярного произведения в SVM
  8. Маржа
  9. Функция оптимизации и ее ограничения
  10. Мягкая маржа SVM
  11. Ядра SVM
  12. Различные типы ядер
  13. Как правильно выбрать ядро ​​в SVM
  14. Реализация и настройка гиперпараметров SVM в Python
  15. Преимущества и недостатки SVM
  16. Конечные примечания

Что такое метод опорных векторов?

Это задача машинного обучения с учителем, в которой мы пытаемся найти гиперплоскость, которая лучше всего разделяет два класса. Примечание: Не путайте SVM и логистическую регрессию. Оба алгоритма пытаются найти лучшую гиперплоскость, но главное отличие состоит в том, что логистическая регрессия является вероятностным подходом, тогда как метод опорных векторов основан на статистических подходах.

Теперь вопрос, какую гиперплоскость он выбирает? Может быть бесконечное количество гиперплоскостей, проходящих через точку и идеально классифицирующих два класса. Итак, какой из них лучший?

Итак, SVM делает это, находя максимальное расстояние между гиперплоскостями, что означает максимальное расстояние между двумя классами.

Когда использовать логистическую регрессию против метода опорных векторов?

В зависимости от количества имеющихся у вас функций вы можете выбрать логистическую регрессию или SVM.

SVM лучше всего работает, когда набор данных небольшой и сложный. Обычно рекомендуется сначала использовать логистическую регрессию и посмотреть, как она работает, если она не дает хорошей точности, вы можете использовать SVM без какого-либо ядра (подробнее о ядрах мы поговорим в следующем разделе). Логистическая регрессия и SVM без ядра имеют одинаковую производительность, но в зависимости от ваших функций один может быть более эффективным, чем другой.

Типы метода опорных векторов

Линейный SVM

Только когда данные идеально линейно разделимы, мы можем использовать Linear SVM. Идеальная линейная разделимость означает, что точки данных можно разделить на 2 класса, используя одну прямую линию (если она двумерная).

Нелинейный SVM

Когда данные не являются линейно разделимыми, мы можем использовать нелинейный SVM, что означает, что когда точки данных не могут быть разделены на 2 класса с помощью прямой линии (если они 2D), тогда мы используем некоторые передовые методы, такие как приемы ядра, для их классификации. . В большинстве реальных приложений мы не находим линейно разделяемых точек данных, поэтому для их решения мы используем трюк ядра.

 

Теперь давайте определим два основных термина, которые будут неоднократно повторяться в этой статье:

Опорные векторы: Это точки, которые находятся ближе всего к гиперплоскости. Разделительная линия будет определена с помощью этих точек данных.

Поле: это расстояние между гиперплоскостью и ближайшими к гиперплоскости наблюдениями (опорными векторами). В SVM большая маржа считается хорошей маржой. Существует два типа полей жесткая маржа и мягкая маржа. Подробнее об этих двух я расскажу в следующем разделе.

Изображение 1

Как работает машина опорных векторов?

SVM определяется таким образом, что он определяется только в терминах опорных векторов, нам не нужно беспокоиться о других наблюдениях, поскольку запас делается с использованием точек, которые находятся ближе всего к гиперплоскости (опорные векторы), тогда как в логистической регрессии классификатор определен по всем точкам. Следовательно, SVM обладает некоторыми естественными ускорениями.
Давайте разберемся с работой SVM на примере. Предположим, у нас есть набор данных с двумя классами (зеленый и синий). Мы хотим классифицировать эту новую точку данных как синюю или зеленую.

Источник изображения: Автор

Чтобы классифицировать эти точки, у нас может быть много границ решений, но вопрос в том, какая из них наилучшая и как ее найти? ПРИМЕЧАНИЕ: Поскольку мы наносим точки данных на двумерный график, мы называем эту границу решения прямой линией , но если у нас есть больше измерений, мы называем эту границу решения «гиперплоскостью»

Источник изображения: Автор

Лучшей гиперплоскостью является та плоскость, которая максимально удалена от обоих классов, и это основная цель SVM. Это делается путем поиска различных гиперплоскостей, которые наилучшим образом классифицируют метки, а затем выбирается та, которая находится дальше всего от точек данных, или та, которая имеет максимальный запас.

Источник изображения: Автор

Математическая интуиция за машиной опорных векторов

Многие люди игнорируют математическую интуицию, стоящую за этим алгоритмом, потому что его довольно сложно переварить. Здесь, в этом разделе, мы постараемся понять каждый шаг работы под капотом. SVM — это широкая тема, и люди все еще проводят исследования этого алгоритма. Если вы планируете проводить исследования, то это может быть неподходящим местом для вас.

Здесь мы поймем только ту часть, которая требуется при реализации этого алгоритма. Вы, должно быть, слышали о первичной формуле , двойной формулировке, множителе Лагранжа 9.0012 и т. д. Я не говорю, что эти темы не важны, но они более важны, если вы планируете проводить исследования в этой области. Давайте двигаться вперед и увидеть магию этого алгоритма.

Прежде чем углубляться в мельчайшие подробности этой темы, давайте сначала разберемся, что такое точечный продукт.

Скалярное произведение

Все мы знаем, что вектор — это величина, которая имеет не только направление, но и величину, и точно так же, как числа, мы можем использовать математические операции, такие как сложение, умножение. В этом разделе мы попытаемся узнать об умножении векторов, которое можно выполнить двумя способами: скалярным произведением и перекрестным произведением. Разница только в том, что скалярное произведение используется для получения в результате скалярного значения, тогда как перекрестное произведение используется для повторного получения вектора.

Скалярное произведение может быть определено как проекция одного вектора на другой, умноженная на произведение другого вектора.

Изображение 2

Здесь a и b — 2 вектора, чтобы найти скалярное произведение между этими 2 векторами, мы сначала находим величину обоих векторов, а чтобы найти величину, мы используем теорему Пифагора или формулу расстояния.

После нахождения величины мы просто умножаем ее на угол косинуса между обоими векторами. Математически это можно записать как:

А . В = |А| cosθ * |B|

Где |А| cosθ — проекция A на B

И |Б| величина вектора B

Теперь в SVM нам нужна только проекция A, а не величина B, позже я объясню почему. Чтобы просто получить проекцию, мы можем просто взять единичный вектор B, потому что он будет в направлении B, но его величина будет равна 1. Следовательно, теперь уравнение принимает вид:

А.В = |А| cosθ * единичный вектор B

Теперь давайте перейдем к следующей части и посмотрим, как мы будем использовать это в SVM.

 

Использование скалярного произведения в SVM:

Рассмотрим случайную точку X, и мы хотим знать, лежит ли она на правой стороне плоскости или на левой стороне плоскости (положительной или отрицательной).

Чтобы найти это, сначала предположим, что эта точка является вектором (X), а затем мы создадим вектор (w), перпендикулярный гиперплоскости. Предположим, что расстояние вектора w от начала координат до границы решения равно «c». Теперь возьмем проекцию вектора X на w.

Мы уже знаем, что проекция любого вектора или другого вектора называется скалярным произведением. Следовательно, мы берем скалярное произведение векторов x и w. Если скалярное произведение больше, чем «с», мы можем сказать, что точка лежит на правой стороне. Если скалярное произведение меньше «с», то точка находится слева, а если скалярное произведение равно «с», то точка лежит на границе решения.

Вы, должно быть, сомневаетесь, почему мы взяли этот перпендикулярный вектор w к гиперплоскости? Итак, нам нужно расстояние вектора X от границы решения, и на границе может быть бесконечное количество точек, от которых можно измерить расстояние. Вот почему мы приходим к стандарту, мы просто берем перпендикуляр и используем его в качестве эталона, а затем берем проекции всех других точек данных на этот перпендикулярный вектор, а затем сравниваем расстояние.

В SVM также есть понятие маржи. В следующем разделе мы увидим, как мы находим уравнение гиперплоскости и что именно нам нужно оптимизировать в SVM.

 

Запас в методе опорных векторов

Все мы знаем, что уравнение гиперплоскости имеет вид w. x+b=0, где w — вектор, нормальный к гиперплоскости, а b — смещение.

Чтобы классифицировать точку как отрицательную или положительную, нам нужно определить решающее правило. Мы можем определить правило принятия решения как:

Если значение w.x+b>0, то мы можем сказать, что это положительная точка, в противном случае это отрицательная точка. Теперь нам нужны (w,b) такие, чтобы поле имело максимальное расстояние. Допустим, это расстояние равно «d».

Для расчета d нам нужно уравнение L1 и L2. Для этого примем несколько предположений, что уравнение L1 равно w.x+b=1 , а уравнение L2 равно w.x+b=-1 . Теперь вопрос приходит

1. Почему величина равная, почему не взяли 1 и -2?

2. Почему мы взяли только 1 и -1, а не любое другое значение, например 24 и -100?

3. Почему мы взяли эту линию?

Попробуем ответить на эти вопросы:

1. Мы хотим, чтобы наша плоскость находилась на одинаковом расстоянии от обоих классов, что означает, что L должна проходить через центр L1 и L2, поэтому мы берем величину равной.

2. Допустим, уравнение нашей гиперплоскости 2x+y=2, мы видим, что даже если мы умножим все уравнение на какое-то другое число, линия не изменится (попробуйте построить на графике). Следовательно, для математического удобства мы принимаем его равным 1,9.0006

3. Теперь главный вопрос, а почему именно эту строку надо считать? Чтобы ответить на этот вопрос, я попытаюсь воспользоваться помощью графиков.

Предположим, что уравнение нашей гиперплоскости 2x+y=2:

Давайте создадим запас для этой гиперплоскости,

Если умножить эти уравнения на 10, мы увидим, что параллельная линия (красная и зеленая) приближается к нашей гиперплоскости. Для большей наглядности посмотрите на этот график (https://www.desmos.com/calculator/dvjo3vacyp)

Мы также наблюдаем, что если мы разделим это уравнение на 10, то эти параллельные линии станут больше. Посмотрите на этот график (https://www.desmos.com/calculator/15dbwehq9).грамм).

Этим я хотел показать вам, что параллельные прямые зависят от (w,b) нашей гиперплоскости, если мы умножим уравнение гиперплоскости с коэффициентом больше 1, то параллельные прямые сожмутся, а если мы умножим с коэффициентом меньше чем 1, они расширяются.

Теперь мы можем сказать, что эти линии будут двигаться, когда мы изменяем (w,b), и вот как это оптимизируется. Но что такое функция оптимизации? Давайте посчитаем.

Мы знаем, что цель SVM состоит в том, чтобы максимизировать этот запас, который означает расстояние (d). Но ограничений на это расстояние (d) немного. Давайте посмотрим, что это за ограничения.

 

Функция оптимизации и ее ограничения

Чтобы получить нашу функцию оптимизации, нужно учесть несколько ограничений. Это ограничение заключается в том, что «Мы рассчитаем расстояние (d) таким образом, чтобы ни одна положительная или отрицательная точка не пересекала предельную линию». Запишем эти ограничения математически:

Вместо того, чтобы использовать 2 ограничения вперед, мы теперь попытаемся упростить эти два ограничения до 1. Мы предполагаем, что отрицательные классы имеют y=-1 и положительные классы имеют y=1 .

Можно сказать, что для правильной классификации каждой точки всегда должно выполняться это условие:

Предположим, что зеленая точка правильно классифицирована, что означает, что она будет следовать w. x+b>=1, , если мы умножим это на y=1 , мы получим то же самое уравнение, упомянутое выше. Точно так же, если мы сделаем это с красной точкой с y=-1 , мы снова получим это уравнение . Следовательно, мы можем сказать, что нам нужно максимизировать (d) так, чтобы это ограничение выполнялось.

Возьмем 2 опорных вектора, 1 из отрицательного класса и 2 и из положительного класса. Расстояние между этими двумя векторами x1 и x2 будет равно (x2-x1) вектору . Что нам нужно, так это кратчайшее расстояние между этими двумя точками, которое можно найти с помощью трюка, который мы использовали в скалярном произведении. Мы берем вектор «w», перпендикулярный гиперплоскости, а затем находим проекцию вектора (x2-x1) на «w». Примечание: этот перпендикулярный вектор должен быть единичным вектором, тогда только это будет работать. Почему это должен быть единичный вектор? Это было объяснено в разделе точечного произведения. Чтобы сделать этот «w» единичным вектором, мы разделим его на норму «w».

Мы уже знаем, как найти проекцию вектора на другой вектор. Мы делаем это скалярным произведением обоих векторов. Итак, давайте посмотрим, как

Так как x2 и x1 являются опорными векторами и лежат на гиперплоскости, то они будут следовать y i * (2.x+b)=1 поэтому мы можем записать это как:

Подставляя уравнения (2) и (3) в уравнение (1) получаем:

Отсюда уравнение, которое мы должны максимизировать:

Теперь мы нашли нашу функцию оптимизации, но здесь есть загвоздка в том, что мы не находим этот тип идеально линейно разделимых данных в отрасли, почти ни в одном случае мы не получаем этот тип данных и, следовательно, мы не можем использовать это условие мы доказали здесь. Тип задачи, которую мы только что изучили, называется Hard Margin SVM теперь мы будем изучать мягкую маржу, которая похожа на эту, но есть еще несколько интересных приемов, которые мы используем в Soft Margin SVM.

 

Мягкая маржа SVM

В реальных приложениях мы не находим ни одного линейно разделимого набора данных, мы находим либо почти линейно разделимый набор данных, либо нелинейно разделимый набор данных. В этом сценарии мы не можем использовать трюк, который мы доказали выше, потому что он говорит, что он будет работать только тогда, когда набор данных полностью линейно разделим.

Чтобы решить эту проблему, мы модифицируем это уравнение таким образом, чтобы оно допускало мало ошибочных классификаций, что означает, что оно допускало неправильную классификацию нескольких точек.

Мы знаем, что max[f(x)] также можно записать как min[1/f(x)] , общепринятой практикой является минимизация функции стоимости для задач оптимизации; следовательно, мы можем инвертировать функцию.

Чтобы составить уравнение с мягкой границей, мы добавляем к этому уравнению еще 2 члена, которые равны дзета 9.0012 и умножить на гиперпараметр c

Для всех правильно классифицированных точек наша дзета будет равна 0, а для всех неправильно классифицированных точек дзета — это просто расстояние этой конкретной точки от ее правильной гиперплоскости, что означает, что если мы видим неправильно классифицированные зеленые точки, значение zeta будет расстоянием этих точек от гиперплоскости L1 и для неправильно классифицированной красной точки zeta будет расстоянием этой точки от гиперплоскости L2.

Итак, теперь мы можем сказать, что это Ошибка SVM = Ошибка маржи + Ошибка классификации. Чем выше маржа, тем меньше возможная маржинальная ошибка, и наоборот.

Допустим, вы берете высокое значение «c» = 1000, это будет означать, что вы не хотите сосредотачиваться на маржинальной ошибке и просто хотите получить модель, которая не классифицирует неправильно ни одну точку данных.

Посмотрите на рисунок ниже.

Если кто-то спросит вас, какая модель лучше, та, где маржа максимальна и есть 2 неправильно классифицированные точки, или та, где маржа очень меньше, и все точки классифицированы правильно?

Ну, на этот вопрос нет правильного ответа, но мы можем использовать SVM Error = Margin Error + Classification Error, чтобы оправдать это. Если вы не хотите, чтобы в модели была какая-либо неправильная классификация, вы можете выбрать рисунок 2 . Это означает, что мы увеличим «c», чтобы уменьшить ошибку классификации, но если вы хотите, чтобы ваша маржа была максимальной, значение «c» должно быть минимальным. Вот почему «с» — это гиперпараметр, и мы находим оптимальное значение «с», используя GridsearchCV и перекрестную проверку.

Давайте двигаться дальше и теперь узнаем об очень хорошем трюке под названием «Трюк с ядром» .

 

Ядра в машине опорных векторов

Самая интересная особенность SVM заключается в том, что он может работать даже с нелинейным набором данных, и для этого мы используем «Kernel Trick», который упрощает классификацию точек. Предположим, у нас есть такой набор данных:

.

Источник изображения: Автор

Здесь мы видим, что не можем провести ни одной линии или, скажем, гиперплоскости, которая могла бы правильно классифицировать точки. Итак, что мы делаем, так это пытаемся преобразовать это пространство более низкой размерности в пространство более высокой размерности, используя некоторые квадратичные функции, которые позволят нам найти границу решения, которая четко разделяет точки данных. Эти функции, которые помогают нам в этом, называются ядрами, и то, какое ядро ​​использовать, определяется исключительно настройкой гиперпараметров.

Изображение 3

Ниже приведены некоторые функции ядра, которые вы можете использовать в SVM:

1. Полиномиальное ядро ​​

Ниже приведена формула ядра полинома:

Здесь d — степень многочлена, которую нам нужно указать вручную.

Предположим, у нас есть две функции X1 и X2 и выходная переменная Y, поэтому, используя полиномиальное ядро, мы можем записать ее как:

Итак, нам нужно найти X 1 2 , X 2 2 и X1.X2, и теперь мы видим, что 2 измерения были преобразованы в 5 измерений.

Изображение 4

2. Сигмовидное ядро ​​

Мы можем использовать его как прокси для нейронных сетей. Уравнение:

Он просто берет ваши входные данные, сопоставляя их со значениями 0 и 1, чтобы их можно было разделить простой прямой линией.

Источник изображения: https://dataaspirant.com/svm-kernels/#t-1608054630725

 

3. Ядро RBF

Что он на самом деле делает, так это создает нелинейные комбинации наших функций, чтобы поднять ваши выборки в многомерное пространство признаков, где мы можем использовать линейную границу решения для разделения ваших классов. Это наиболее часто используемое ядро ​​в классификациях SVM, следующее формула объясняет это математически:

где,

1. «σ» — это дисперсия и наш гиперпараметр
2. || Х₁ – Х₂ || — Евклидово расстояние между двумя точками X₁ и X₂

Изображение 5

4. Ядро функции Бесселя

В основном используется для устранения перекрестного члена в математических функциях. Ниже приведена формула ядра функции Бесселя:

5. Ядро Anova

Он хорошо работает с задачами многомерной регрессии. Формула для этой функции ядра:

 

Как правильно выбрать ядро?

Мне хорошо известно, что у вас должны быть сомнения относительно того, как решить, какая функция ядра будет эффективно работать с вашим набором данных. Необходимо выбрать хорошую функцию ядра, поскольку от этого зависит производительность модели.

Выбор ядра полностью зависит от того, с каким набором данных вы работаете. Если это линейно разделимо, вы должны выбрать. для линейной функции ядра, так как она очень проста в использовании, а сложность намного ниже по сравнению с другими функциями ядра. Я бы рекомендовал вам начать с гипотезы о том, что ваши данные линейно разделимы, и выбрать линейную функцию ядра.

Затем вы можете перейти к более сложным функциям ядра. Обычно мы используем SVM с RBF и линейной функцией ядра, потому что другие ядра, такие как полиномиальное ядро, используются редко из-за низкой эффективности. Но что, если и линейный, и RBF дают примерно одинаковые результаты? Какое ядро ​​теперь выбираем? Давайте разберемся с этим на примере, для простоты я возьму только 2 функции, которые означают только 2 измерения. На рисунке ниже я нанес границу решения линейного SVM для 2 функций набора данных радужной оболочки:

 

Изображение 6

Здесь мы видим, что линейное ядро ​​отлично работает на этом наборе данных, а теперь посмотрим, как будет работать ядро ​​RBF.

Изображение 7

Мы видим, что оба ядра дают одинаковые результаты, оба хорошо работают с нашим набором данных, но какое из них выбрать? Линейный SVM — это параметрическая модель. Параметрическая модель — это концепция, используемая для описания модели, в которой все ее данные представлены в ее параметрах. Короче говоря, единственная информация, необходимая для прогнозирования будущего на основе текущего значения, — это параметры.

Сложность ядра RBF возрастает по мере увеличения размера обучающих данных. В дополнение к тому, что подготовка ядра RBF обходится дороже, мы также должны поддерживать матрицу ядра, а проекция в это «бесконечное» многомерное пространство, где данные становятся линейно разделимыми, также обходится дороже во время прогнозирования. Если набор данных нелинейный, то использование линейного ядра не имеет смысла, мы получим очень низкую точность, если сделаем это.

Изображение 8

Таким образом, для такого набора данных мы можем использовать RBF даже не задумываясь, потому что он определяет границы решения следующим образом:

Изображение 9

Внедрение и настройка гиперпараметров машины опорных векторов в Python

Для реализации набора данных мы будем использовать набор данных Income Evaluation, содержащий информацию о личной жизни человека и вывод 50 000 или <= 50. Набор данных можно найти здесь (https://www.kaggle.com/lodetomasi1995/income-classification)

.

Задача здесь состоит в том, чтобы классифицировать доход человека при наличии необходимых исходных данных о его личной жизни.

Сначала импортируем все необходимые библиотеки.

 # Импорт всех соответствующих библиотек

из sklearn.svm импортировать SVC

импортировать numpy как np

импортировать панд как pd

из sklearn.preprocessing импортировать StandardScaler

из sklearn.model_selection импорта train_test_split

импорт из sklearn.metrics: точность_оценки, путаница_матрица

предварительная обработка импорта из sklearn

предупреждения об импорте

предупреждения.filterwarnings("игнорировать")

Теперь давайте прочитаем набор данных и посмотрим на столбцы, чтобы лучше понять информацию.

df = pd.read_csv('income_evaluation.csv') 
 df.head()

 

Я уже сделал часть предварительной обработки данных, и вы можете посмотреть весь код здесь. Здесь моя основная цель — рассказать вам, как реализовать SVM на python.

Теперь для обучения и тестирования нашей модели данные должны быть разделены на обучающие и тестовые данные.
Мы также будем масштабировать данные, чтобы они находились в диапазоне от 0 до 1.

 # Разделить набор данных на тестовые и обучающие данные 
 X_train, X_test, y_train, y_test = train_test_split(df.drop('доход', ось=1),df['доход'], test_size=0,2)

Теперь давайте продолжим определение классификатора опорных векторов вместе с его гиперпараметрами. Далее мы подгоним эту модель к обучающим данным.

 # Определить классификатор опорных векторов с гиперпараметрами 
 svc = SVC (случайное_состояние = 101) 
 точности = cross_val_score(svc,X_train,y_train,cv=5) 
 svc.fit(X_train,y_train) 
 print("Оценка поезда:"np.mean(точность)) 
 printf("Оценка теста:" svc.score(X_test,y_test))

Модель обучена, и теперь мы также можем наблюдать за выходными данными.

Ниже вы можете увидеть точность набора данных теста и обучения

 

Вы даже можете гипертюнинговать свою модель по следующему коду:

 сетка = {
 'С':[0.01,0.1,1,10], 
 'ядро' : ["линейный","поли","rbf","сигмоид"], 
 'степень' : [1,3,5,7], 
 'гамма': [0.01,1] 
 } 
 свм = СВК () 
 svm_cv = GridSearchCV (svm, сетка, cv = 5) 
 svm_cv.fit(X_train,y_train) 
 печать ("Лучшие параметры:", svm_cv.best_params_) 
 print("Оценка поезда:", svm_cv.best_score_) 
 print("Оценка теста:", svm_cv.score(X_test,y_test))

 

Набор данных довольно большой, и, следовательно, потребуется время для обучения, по этой причине я не могу вставить сюда результат приведенного выше кода, потому что SVM плохо работает с большими наборами данных, требуется много времени, чтобы получить обученный.

Преимущества SVM

1. SVM работает лучше, когда данные являются линейными

2. Более эффективен в больших размерах

3. С помощью трюка с ядром мы можем решить любую сложную проблему

4. SVM не чувствителен к выбросам

5. Может помочь нам с классификацией изображений

Недостатки SVM

1. Выбрать хорошее ядро ​​непросто

2. Не показывает хороших результатов на большом наборе данных

3. Гиперпараметрами SVM являются Cost-C и gamma. Не так-то просто точно настроить эти гиперпараметры. Трудно представить себе их влияние

Конец Примечания

В этой статье мы подробно рассмотрели очень мощный алгоритм машинного обучения, метод опорных векторов. Я обсудил его концепцию работы, математическую интуицию за SVM, реализацию на питоне, приемы классификации нелинейных наборов данных, плюсы и минусы, и, наконец, мы решили проблему с помощью SVM.

Об авторе

В настоящее время я учусь на последнем курсе по статистике (бакалавр статистики) и проявляю большой интерес к области науки о данных, машинного обучения и искусственного интеллекта. Мне нравится погружаться в данные, чтобы обнаруживать тенденции и другие ценные сведения о данных. Я постоянно учусь и мотивирован пробовать что-то новое.

Открыт к сотрудничеству и работе.

По любым вопросам и сомнениям, не стесняйтесь обращаться ко мне по электронной почте

Свяжитесь со мной в LinkedIn и Twitter

Источник изображения:

  • Изображение 1: https://www.javatpoint.com/machine-learning-support-vector-machine-algorithm
  • Изображение 2: https://byjus.com/maths/dot-product-of-two-vectors/
  • Изображение 3: https://medium.com/@zxr.nju/what-is-the-kernel-trick-why-is-it-important-98a98db0961d
  • Изображение 4: https://www.oreilly.com/library/view/machine-learning-quick/9781788830577/fc007e8f-36a8-4d27-8e22-5d4d82270cdf.xhtml
  • Изображение 5: https://dataaspirant.com/svm-kernels/#t-1608054630725
  • Изображение 6: https://www.kdnuggets.com/2016/06/select-support-vector-machine-kernels.html
  • Изображение 7: https://www. kdnuggets.com/2016/06/select-support-vector-machine-kernels.html
  • Изображение 8: https://www.kdnuggets.com/2016/06/select-support-vector-machine-kernels.html
  • Изображение 9: https://www.kdnuggets.com/2016/06/select-support-vector-machine-kernels.html

 

Медиафайлы, показанные в этой статье, не принадлежат Analytics Vidhya и используются по усмотрению Автора.

Полное руководство по поддержке векторных машин (SVM) | by KUSHAL CHAKRABORTY

Машина опорных векторов — популярный алгоритм машинного обучения, ставший популярным в конце 90-х годов. Это контролируемый алгоритм машинного обучения, который можно использовать как для классификации , так и для регрессии .

С точки зрения классификации, это дискриминативный классификатор, который используется для поиска оптимальной гиперплоскости для распределения данных по разным классам. В двумерном пространстве эту оптимальную гиперплоскость можно представить как линию, разделяющую пространство на две части: где одна часть пространства содержит точки данных, принадлежащие одному классу, а другая часть пространства содержит точки данных, принадлежащие другому классу. учебный класс. Концепция линий, действующих как классификатор, верна только в том случае, если точки данных линейно разделимы. SVM также можно использовать для поиска оптимальной кривой, которую можно использовать для классификации точек данных, которые не являются линейно разделимыми.

С точки зрения регрессии, его можно использовать для подгонки кривой или линии к ряду точек данных.

Мы объясним каждое из этих понятий на примерах в следующих разделах.

В этом разделе мы подробно рассмотрим приведенные выше определения и концепции с некоторыми примерами.

Для нашего удобства мы объясним понятия, относящиеся к двумерному пространству и линиям, которые можно распространить на более чем двумерное пространство и гиперплоскости.

Рисунок 1: h2 не разделяет классы. h3 делает, но с небольшим отрывом. h4 разделяет их с максимальным отрывом.( Источник : www.wikipediacom/SVM )

Рассмотрим приведенный выше рисунок. Здесь у нас есть два типа точек данных. Учтите, что точки данных, отмеченные черным цветом, относятся к положительному классу, а точки данных, отмеченные черной рамкой, относятся к отрицательному классу. У нас есть три прямые линии, которые могут разделить точки данных на два класса, но главный вопрос: «Какая прямая лучше всего подходит для задачи классификации?» .

2.1 Геометрическая интуиция о SVM

В предыдущих разделах мы использовали термин «оптимальная гиперплоскость». В этом разделе мы объясним, что мы подразумеваем под «оптимальной гиперплоскостью».

Под оптимальной гиперплоскостью мы подразумеваем ту разделяющую гиперплоскость, от которой точки данных классов находятся на максимальном расстоянии с обеих сторон.

Оптимальная гиперплоскость определяется плоскостью, которая максимизирует перпендикулярное расстояние между гиперплоскостью и ближайшими образцами. Это перпендикулярное расстояние может быть натянуто опорными векторами.

Теперь мы введем термин под названием «маржа» . Давайте рассмотрим приведенный ниже рисунок 2.

Рисунок 2: Рисунок, показывающий положительные, отрицательные и разделяющие гиперплоскости, опорные векторы и поля. ( Источник : https://1.bp.com/-K8qVBF8FKpk/WVnU0CDKPzI/AAAAAAAABy )

Мы видим, что есть три гиперплоскости:

  • Гиперплоскость, которая касается точек положительный класс называется положительной гиперплоскостью .
  • Гиперплоскость, которая касается точек отрицательного класса, называется отрицательной гиперплоскостью .
  • Гиперплоскость, расположенная между положительным и отрицательным классом, называется , разделяющей гиперплоскостью .
  • Все эти три гиперплоскости параллельны друг другу.

Расстояние между положительной и отрицательной гиперплоскостью называется «полем ». Если мы максимизируем запас, то положительные и отрицательные точки будут довольно далеко друг от друга, а также от разделяющей гиперплоскости. Следовательно, точность задачи классификации возрастает. Чем шире поле, тем лучше оно подходит для задачи классификации. По мере увеличения маржи «точность обобщения» (точность модели в будущих невидимых точках данных) увеличивается.

SVM пытаются найти гиперплоскость, которая максимизирует запас. Следовательно, оптимальная или разделяющая гиперплоскость также называется «гиперплоскостью, максимизирующей запас».

Следовательно, на рисунке 1 гиперплоскость h4 является лучшей гиперплоскостью.

2.2 Опорные векторы

Опорные векторы — это точки данных, которые касаются положительной и отрицательной гиперплоскостей. На рисунке 2 мы видим, что есть некоторые точки данных, которые сначала касаются положительной и отрицательной гиперплоскостей, эти точки данных известны как 9. 0098 «Опорные векторы» .

Примечание: Для будущих невидимых точек данных мы будем использовать положение, направление и сторону точки данных только относительно разделяющей гиперплоскости, чтобы определить класс точек данных (а не положительные и отрицательные гиперплоскости).

2.3 Альтернативная геометрическая интуиция о SVM

В этом разделе мы будем использовать концепцию «Выпуклая оболочка» , чтобы найти максимизирующую запас гиперплоскость .

Выпуклая оболочка может быть определена как наименьший выпуклый многоугольник, все точки которого находятся либо внутри многоугольника, либо на многоугольнике.

Рисунок 3. Схема выпуклой оболочки ( Источник: https://www.geeksforgeeks.org)

Выпуклый многоугольник — это, по существу, такой многоугольник, что все точки кратчайшей линии, соединяющей любые две точки (расположенные внутри или на polygon) лежит внутри или на многоугольнике.

Чтобы найти гиперплоскость, максимизирующую запас, используя концепцию выпуклой оболочки, мы будем использовать следующие шаги:

  • Сначала нарисуйте выпуклую оболочку для положительных точек данных.
  • Во-вторых, нарисуйте выпуклую оболочку для отрицательных точек данных.
  • В-третьих, найдите кратчайшую линию или гиперплоскость, соединяющую корпуса.
  • Наконец, нарисуйте линию или гиперплоскость, которая делит пополам линию или гиперплоскость (нарисованную на третьем шаге). Эта полученная линия или гиперплоскость называется «гиперплоскостью, максимизирующей запас» .

Рис. 4. Разделяющая гиперплоскость, полученная с использованием концепции выпуклой оболочки (Источник: https://sciencedirect.com)

Предположим, что положительная и отрицательная гиперплоскости находятся на единичном расстоянии от разделяющей гиперплоскости.

3.1 SVM с жесткими границами

3.2 SVM с мягкими границами

вторая часть упоминается как «Потеря шарнира» .

‘C’ — это гиперпараметр, который всегда имеет положительное значение. Если «C» увеличивается, то увеличивается переобучение, а если «C» уменьшается, то увеличивается недообученность. Для больших значений «C» оптимизация выберет гиперплоскость с меньшим запасом, если эта гиперплоскость лучше справляется с правильной классификацией всех обучающих точек. И наоборот, очень маленькое значение «C» заставит оптимизатор искать разделяющую гиперплоскость с большим запасом, даже если эта гиперплоскость неправильно классифицирует больше точек.

Разделяющая гиперплоскость с низким значением «C». ( Источник : https://jmlr.com/machine-learning-svm) Разделяющая гиперплоскость с высоким значением «C». ( Источник : https://jmlr.com/machine-learning-svm) Рисунок 6: График потерь в шарнирах

Примечание. Можно доказать, что уравнение оптимизации, полученное в этом разделе, и полученное уравнение оптимизации в предыдущем разделе такие же. Только C и лямбда обратно пропорциональны друг другу, т.е.

C = 1/лямбда

Ядро — это способ вычисления скалярного произведения двух векторов x и y в некотором (возможно, очень многомерном) пространстве признаков, поэтому функции ядра иногда называют «обобщенным скалярным произведением». ».

Ядро полезно, потому что оно дает нам возможность вычислять скалярные произведения в некотором пространстве признаков, даже не зная, что это за пространство и что такое фи.

Теперь рассмотрим, что если бы у нас были данные, как показано на рисунке ниже? Ясно, что нет линии, которая могла бы разделить два класса в этой плоскости x-y. Так что же нам делать? Мы применяем трансформацию и добавляем еще одно измерение, которое мы называем осью Z. Допустим значение точек на плоскости z, w = x² + y². В этом случае мы можем манипулировать им как расстоянием точки от z-начала. Теперь, если мы построим по оси Z, будет видно четкое разделение, и можно будет провести линию.

Рисунок 7. Можем ли мы провести разделительную линию в этой плоскости? (Источник: https: // глава-2-svm-support-vector-machine-theory-f0812effc72) Рисунок 8: график оси z-y. Здесь можно провести разделение. (Источник: https: // глава-2-svm-support-vector-machine-theory-f0812effc72)

Когда мы преобразуем эту линию обратно в исходную плоскость, она сопоставляется с круговой границей, как показано на изображении ниже.

Рис. 9. При обратном преобразовании в плоскость x-y линия превращается в окружность. (Источник: https: // глава-2-svm-support-vector-machine-theory-f0812effc72)

В приведенном выше примере ядро ​​будет внутренне и неявно преобразовывать данные, которые являются 2D, в другое пространство более высокого измерения. где данные станут линейно разделимыми.

Что делает кернализация, так это то, что она берет данные размерности «d» и внутренне и неявно преобразует функцию, используя трюк ядра, в размерность «d1», обычно где d1 > d. В «d1» данные становятся линейно разделимыми.

Цифра 7 явно не является линейно разделимой, но если мы попытаемся отобразить ее в трехмерном пространстве, используя:

(Ссылка: https://people.eecs.berkeley.edu/~jordan/courses/)

Если мы хотим узнать больше о матрице граммов, вы можете обратиться сюда.

Итак, если у нас есть функция «K», определенная следующим образом:

, тогда нам просто нужно знать K , а не саму функцию отображения. Эта функция известна как функция ядра и снижает сложность поиска функции отображения. Итак, Функция ядра определяет внутренний продукт в преобразованном пространстве.

Мы должны выбрать правильное ядро ​​на основе нашего приложения. Существуют различные типы ядер:

Теорема Мерсера

Помимо этих предопределенных ядер, какие условия определяют, какие функции можно считать ядрами? Это дается теоремой Мерсера.

Первое условие довольно тривиально, т. е. функция ядра должна быть симметричной. Поскольку функция ядра является скалярным произведением (внутренним произведением) функции отображения, мы можем написать следующее:

Теорема Мерсера подводит нас к необходимому и достаточному условию для того, чтобы функция была функцией ядра.

(Ссылка: https://people.eecs.berkeley.edu/~jordan/courses/)

Сложность времени обучения SVM составляет приблизительно O(n²). Если n очень велико, то O(n²) также очень велико, поэтому SVM не используются в приложениях с малой задержкой.

Сложность выполнения приблизительно равна O(k.d), где

k = количество опорных векторов

d = размерность данных

Машина опорных векторов также может использоваться в качестве метода регрессии, сохраняя все основные характеристики, характеризующие алгоритм (максимальная маржа). Регрессия опорных векторов (SVR) использует для классификации те же принципы, что и SVM, с небольшими отличиями. Прежде всего, поскольку выход представляет собой действительное число, становится очень трудно предсказать имеющуюся информацию, которая имеет бесконечные возможности. В случае регрессии предел допуска (эпсилон) устанавливается в приближении к SVM, который уже был запрошен из задачи. Но помимо этого факта есть и более сложная причина, алгоритм сложнее, поэтому нужно учитывать. Однако основная идея всегда одна и та же: свести к минимуму ошибку, индивидуализировав гиперплоскость, которая максимизирует запас, помня о том, что часть ошибки допустима.

Линейный SVR ( Источник : https://www.saedsayad.com/support_vector_machine_reg.htm )

В SVC есть очень важный гиперпараметр, называемый « гамма », который используется очень часто.

Гамма : Параметр гаммы определяет, насколько далеко простирается влияние одного обучающего примера, при этом низкие значения означают «далеко», а высокие значения означают «близость». Другими словами, при низкой гамме точки, находящиеся далеко от вероятной линии разделения, учитываются при расчете линии разделения. Поскольку высокая гамма означает, что при расчете учитываются точки, близкие к правдоподобной линии. 92 представляет собой квадрат евклидова расстояния между двумя точками данных x и x ‘.

Если значение сигмы поддерживается постоянным, по мере увеличения расстояния между точками значение K(x,x’) уменьшается экспоненциально и, следовательно, сходство уменьшается.

Поведение функции ядра RBF с сигмой

Теперь, если мы сохраним расстояние постоянным и изменим сигму, из приведенного выше рисунка можно увидеть, что:

. Интуитивно это означает, что если мы увеличим сигму, расстояние, в пределах которого точки будут считаться имеющими значение сходства больше 0, увеличится (любые другие точки, находящиеся на расстоянии большем, чем это, будут иметь значение сходства, равное 0) и наоборот.

Однако важно только знать, что классификатор SVC, использующий ядро ​​RBF, имеет два параметра: ‘ gamma ’ и ‘ C ’.

Мы объяснили эти два параметра в предыдущих разделах.

Гамма = 0,01 и C = 1

Гамма = 1,0 и C = 1,0

Гамма = 10,0 и C = 1,0

Гамма = 100,0 и C = 1,0

C = 10 и гамма = 0,01

Наблюдатель: Наблюдатель: 100009 C = 10 и гамма = 0,01

9000 2 . «гамма» — это параметр ядра RBF, и его можно рассматривать как «разброс» ядра и, следовательно, область принятия решений. Когда «гамма» низкая, «кривая» границы решения очень низкая, и, таким образом, область решения очень широкая. Когда «гамма» высока, «кривая» границы решения высока, что создает островки границ решения вокруг точек данных.

‘C’ — это параметр учащегося SVC и штраф за неправильную классификацию точки данных. Когда ‘C’ мало, классификатор в порядке с неправильно классифицированными точками данных (высокое смещение, низкая дисперсия). Когда ‘C’ большой, классификатор сильно наказывается за ошибочную классификацию данных и, следовательно, избегает любых ошибочно классифицированных точек данных (низкое смещение, высокая дисперсия).

9.1 Внедрение SVM на наборе данных Real World

В этом разделе мы реализуем SVM на донорах Выберите набор данных . В этом разделе мы будем использовать функции SVM, предоставляемые библиотекой sklearn.

Подробную информацию о наборе данных можно найти здесь. Это проблема, основанная на классификации.

Для SVM ядра мы можем использовать SVC(), предоставляемую библиотекой sklearn. Вы можете получить подробную документацию об этом здесь.

Для линейных SVM мы можем использовать SGDClassifier (потеря = ‘шарнир’), предоставленный библиотекой sklearn. Вы можете получить подробную документацию об этом отсюда.

Мы использовали следующие шаги, чтобы применить линейный SVM к донорам. Выберите набор данных:

  1. Разделите набор данных на обучающий и тестовый наборы данных.
  2. Затем мы выполнили настройку гиперпараметров, чтобы найти лучшие гиперпараметры с использованием метода перекрестной проверки. Здесь у нас есть GridSearchCV(), предоставленный библиотекой sklearn.

Настройка гиперпараметров с использованием перекрестной проверки поиска по сетке

Несмотря на наличие различных гиперпараметров, мы использовали два основных гиперпараметра: альфа, штраф (или термин регуляризации)

3. Затем мы создаем модель с лучшие гиперпараметры.

4. Теперь мы оцениваем производительность модели, используя тестовый набор данных. Показателем оценки, который мы использовали здесь, является оценка «roc auc», поскольку это несбалансированный набор данных.

Фрагмент кода, показывающий создание модели с использованием лучших гиперпараметров и оценку модели Графики ROC AUC с оценками AUC для данных обучения и испытаний /en.wikipedia.org/wiki/Support-vector_machine

  • https://www.geeksforgeeks.org/convex-hull-set-1-jarviss-algorithm-or-wrapping/
  • https://www.sciencedirect. com/science/article/pii/S0925231213006449
  • https://www.