Форма сзв м дополняющая: Дополняющая форма СЗВ-М: как заполнить, буде ли штраф

СЗВ-М. Ежемесячная форма отчетности в ПФ. / Контур.Зарплата / СКБ Контур

  1. Контур.Зарплата
  2. Отчетность

  3. Статьи

    Форма СЗВ-М, форма ежемесячной отчетности.

    — Введена обязанность представлять сведения «Федеральный закон от 29.12.2015 № 385-ФЗ «О приостановлении действия отдельных положений законодательных актов Российской Федерации, внесении изменений в отдельные законодательные акты Российской Федерации и особенностях увеличения страховой пенсии, фиксированной выплаты к страховой пенсии и социальных пенсий» http://publication.pravo.gov.ru/Document/View/0001201512290017

    — Постановление Правления ПФ РФ от 01.02.2016 N 83п «Об утверждении формы «Сведения о застрахованных лицах» (Зарегистрировано в Минюсте России 18.02.2016 N 41142)

    — Формат утвержден «Распоряжение Правления ПФ РФ от 25.02.2016 N 70р «Об утверждении формата данных сведений о застрахованных лицах».

    — Форма предоставляется с 1 по 10 число месяца следующего за отчетным.

    — Правила по документообороту для СЗВ-М такие как для остальных форм.

    В форме содержится информация о сотрудниках:

    • которые заключили с работодателем трудовой или гражданско-правовой договор.
    • если сотрудник числился на работе хоть 1 день, пусть даже он этим днем был уволен, даже если он в декрете или в административном отпуске.
    • если договор бессрочный, то сотрудник отражается в СЗВ-М в том месяце, когда будет подписан акт выполненных работ. Важно, чтобы данные о сотруднике помесячно совпадали в РСВ и СЗВ-М, для избежания штрафов это определяющее соответствие.
    • Форма СЗВ-М сдается в электронном виде если, количество сотрудников в организации больше 25. Иначе можно сдать на бумаге, для этого нужно 2 экземпляра печатных + электронный носитель с файлом.
    • На пачки не делится. 1 Файл — 1 Посылка — 1 Тип.
    • Номера сотрудников в форме должны идти строго по порядку, начиная с 1, без пропусков и повторений.
    • Проверка осуществляется по ФИО и СНИЛС. ИНН если вводить, то только правильный, фиктивные ИНН нельзя заполнять.
    • Могут быть 3 типа данной формы исходная / дополняющая / отменяющая
    1. Исходная — подается если форма не подавалась или не была загружена в базу ПФР( пришел отрицательный протокол Check ПФР по другому мы не можем определить загружен в базу отчет или нет).
    2. Дополняющая — подается в том случае, если форма принята и найдены ошибки самим страхователем или инспектором ПФ. В форму включаются только те сотрудники, по которым были ошибки, или которых забыли включить в исходный отчет.
    3. Отменяющая — подается в том случае, если данные на сотрудника не нужно было сдавать в данный ПФ, а пользователь отправил и их приняли.

    Формирование в Контур.Зарплате:

    1. Исходная — Отчеты — Отчеты в Пенсионный фонд — Исходный отчет — СЗВ-М
    2. Дополняющая — Отчеты — Отчеты в Пенсионный фонд — Корректирующий отчет — СЗВ-М — Корректирующие.
    3. Отменяющая — Отчеты — Отчеты в Пенсионный фонд — Корректирующий отчет — СЗВ-М — Отменяющие.

    Настройки в Контур-Зарплате.

    Настройки формы находятся в пункте меню Настройка — Настройка таблиц и форм — Справки и отчеты для ПФ — СЗВ-М.

    Часто используемые настройки:

    • Учитывать только даты приема-увольнения — при значении 0 попадает работник в СЗВ-М или нет определяется по трудовому стажу, при значении 1 только по датам приема/увольнения.
    • Учет сумм — при значении 0 — наличие сумм не влияет на попадание сотрудника в отчет, при значении 1 — как учитываются суммы определяется настройкой РСВ.
    • Сортировка списка работников — 0 — не сортировать, 1 — сортировать по ФИО, 2 — по СНИЛС.

    Предыдущая статья: Как в программе Контур.Зарплата вести электронные трудовые книжки и формировать отчет СЗВ-ТД.

    Следующая статья: Формирование отчета «СЗВ-стаж» в программе Контур. Зарплата

    Эта статья помогла Вам?

    Двойственность для SVM — Математика ∩ Программирование

    Этот пост является продолжением статьи «Формулирование задачи оптимизации метода опорных векторов».

    Теорема Каруша-Куна-Таккера

    Общие задачи оптимизации трудно решить эффективно. Однако задачи оптимизации, цель и ограничения которых имеют особую структуру , часто поддаются аналитическим упрощениям. Например, если вы хотите оптимизировать линейную функцию с учетом ограничений линейного равенства, можно вычислить лагранжиан системы и найти нули ее градиента. В более общем смысле, оптимизация линейной функции с учетом ограничений линейного равенства и неравенства может быть решена с использованием различных так называемых методов «линейного программирования», таких как симплексный алгоритм.

    Однако, когда цель не является линейной, как в случае с SVM, все становится сложнее. Точно так же, если ограничения не образуют выпуклого множества, вам (обычно) не повезло с точки зрения анализа. Вы должны вернуться к числовым методам и скрестить пальцы. Обратите внимание, что множество точек, удовлетворяющих набору линейных неравенств, образует выпуклое множество при условии, что все они могут быть удовлетворены.

    Нам повезло. Задача SVM может быть выражена как так называемая «выпуклая квадратичная» задача оптимизации, означающая, что цель представляет собой квадратичную функцию, а ограничения образуют выпуклый набор (линейные неравенства и равенства). Есть изящная теорема, которая касается таких случаев, и это «выпукло-квадратичное» обобщение метода Лагранжа. Результат получен благодаря Карушу, Куну и Такеру (названный теоремой ККТ), но мы сформулируем более конкретный случай, непосредственно применимый к SVM. 9n$ следующего вида:

    $ \displaystyle \min f(x), \text{ при условии } g_i(x) \leq 0, i = 1, \dots, m$

    Где $f$ — дифференцируемые функции входных переменных $x$ и $g_1,\dots,g_m$ аффинны (многочлены степени 1). Предположим, что $z$ является локальным минимумом $f$. Тогда существуют константы (называемые ККТ или множителями Лагранжа) $ \alpha_1, \dots, \alpha_m$ такие, что выполняются следующие условия. Обратите внимание, что метки в скобках содержат много преднамеренно не определенных терминов.

    9m \alpha_i \nabla g_i(z)$ (градиент лагранжиана равен нулю)

  • $ g_i(z) \leq 0$ для всех $ i = 1, \dots, m$ (основные ограничения выполнены)
  • $ \alpha_i \geq 0$ для всех $ i = 1, \dots, m$ (выполнены двойные ограничения)
  • $ \alpha_i g_i(z) = 0$ для всех $ i = 1, \dots, m$ (дополнительные условия нежесткости)

    • Мы сейчас обсудим, как интерпретировать эти условия, но сначала несколько отступлений. Большая часть работы в SVM заключается в преобразовании исходной геометрической постановки задачи о максимизации поля линейного разделителя в форму, подходящую для этой теоремы. Мы сделали это в прошлый раз. Однако условия этой теоремы также обеспечивают структуру для более аналитического алгоритма, алгоритма последовательной минимальной оптимизации, который позволяет нам избегать численных методов. Мы увидим, как это работает явно, в следующий раз, когда будем реализовывать SMO.

    Возможно, вы помните, что для базового лагранжиана каждое ограничение в задаче оптимизации соответствует одному множителю Лагранжа и, следовательно, одному члену лагранжиана. Здесь все практически то же самое: каждое ограничение в задаче SVM (и, следовательно, каждая обучающая точка) соответствует множителю KKT, но, кроме того, каждый множитель KKT соответствует ограничению   для новой задачи оптимизации, которую неявно определяет эта теорема (называемой двойная проблема). Таким образом, псевдокод алгоритма последовательной минимальной оптимизации состоит в том, чтобы начать с некоторой произвольной разделяющей гиперплоскости $w$ и найти любую обучающую точку $x_j$, которая соответствует нарушенному ограничению. Исправьте $ w$ так, чтобы он работал для $ x_j$, и повторяйте до тех пор, пока не перестанете находить нарушенные ограничения.

    Теперь интерпретируем эти четыре условия. Трудность в этой части обсуждения заключается в понятии первичных/двойственных задач.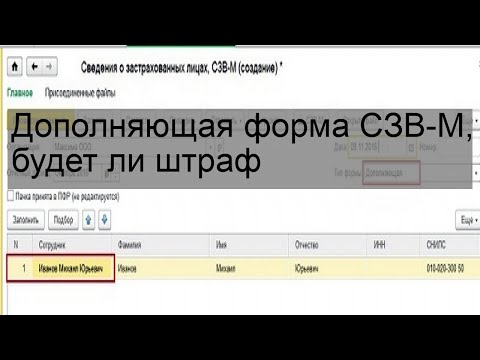 «Исходную» задачу оптимизации часто называют «первой» задачей. В то время как «основная задача» может быть либо минимизацией, либо максимизацией (и для каждого из них существует соответствующая теорема ККТ), мы будем использовать одну из форм:

    $ \displaystyle \min f(x), \text{ при условии } g_i(x) \leq 0, i = 1, \dots, m$

    Далее мы определяем соответствующую «двойственную» задачу оптимизации, которая представляет собой максимизация задача, цель и ограничения которой связаны с первичным стандартным, но утомительным для записи способом. В общем случае эта задача двойной максимизации гарантирует, что ее оптимальное решение (a max) является нижней границей оптимального решения для простого числа (a min). Это может быть полезно во многих настройках. В самых приятных условиях, включая SVM, вы получаете еще более сильную гарантию того, что оптимальные решения для прямой и двойной задач имеют одинаковое объективное значение . То есть граница, которую двойная цель обеспечивает для первичного оптимума, жесткая. В этом случае первичный и двойственный – это два эквивалентных взгляда на одну и ту же проблему. Решение двойственного дает решение первичного, и наоборот.

    Теорема ККТ неявно определяет двойственную проблему, что может быть ясно из формулировки теоремы только в том случае, если вы уже близко знакомы с дуальными и лагранжианами. Эта двойная задача имеет переменные $ \alpha = (\alpha_1, \dots, \alpha_m)$, по одной записи для каждого ограничения первичного числа. Для ККТ двойственными ограничениями являются просто неотрицательность переменных 9m \alpha_i g_i(x)$

    Хотя надлежащее обсуждение первичности и двойственности могло бы занять целую книгу, на этом нам придется остановиться. Если вы хотите углубиться в эту кроличью нору, эти заметки представляют собой отличное введение с точки зрения классического лагранжиана без каких-либо шрамов.

    Но мы можем начать понимать, почему условия KKT такие, какие они есть. Первый требует, чтобы обобщенный лагранжиан имел нулевой градиент. Как и в случае с классическими лагранжианами, это означает, что основная цель находится в локальном минимуме. Второй требует, чтобы ограничения основной задачи были удовлетворены. Третий делает то же самое для двойных ограничений. Четвертый интересен, потому что в нем говорится, что в оптимальном решении первичное и двойственное ограничения переплетаются.

    4. $ \alpha_i g_i(z) = 0$ для всех $ i = 1, \dots, m$ (дополнительные условия нежесткости)

    Более конкретно, эти условия «дополнительной нежесткости» требуют, чтобы для каждого $ i$ либо двойное ограничение $ \alpha_i \geq 0$ на самом деле жесткое ($ \alpha_i = 0$), либо прямое ограничение $g_i$ жесткое. Хотя бы одно из двух должно быть точно на пределе (равно нулю, не строго меньше). Уловка «произведение равно нулю означает, что один множитель равен нулю» здесь пригодится, чтобы выразить ИЛИ, несмотря на то, что преследует поколения студентов, изучающих элементарную алгебру. В терминах задачи SVM комплементарная нежесткость означает, что для оптимальной разделяющей гиперплоскости $w$, если точка данных не имеет функционального запаса ровно 1, то эта точка данных не является опорным вектором. Действительно, когда $ \alpha_i = 0$, мы увидим в следующем разделе, как это влияет на соответствующую обучающую точку $ x_i$. 9м \alpha_j y_j x_j$. Это интересно! Критерий оптимальности, заключающийся в том, что градиент лагранжиана должен быть равен нулю, на самом деле показывает нам, как записать оптимальное решение $ w$ в терминах множителей Лагранжа $ \alpha_j$ и обучающих данных/меток. Это также намекает на то, что из-за этого условия дополнительной нежесткости многие из $\alpha_i$ окажутся равными нулю, и, следовательно, оптимальное решение можно записать в виде разреженных сумм обучающих примеров.

    И теперь, когда мы записали $w$ через $\alpha_j$, мы можем исключить $w$ из формулы для лагранжиана и получить цель двойной оптимизации только через $\alpha_j$. Подставляя (и объединяя полученные две двойные суммы с коэффициентами $\frac{1}{2}$ и $-1$), получаем 9m \alpha_i \alpha_j y_i y_j \langle x_i, x_j \rangle$

    Снова предвещая, что эта форма зависит только от скалярных произведений тренировочных точек, позволит нам заменить стандартное (линейное) скалярное произведение на нелинейное функция, подобная внутреннему продукту, называемая ядром , которая позволит нам ввести нелинейность в границу решения.

    Вернемся к дифференцированию лагранжиана. Для остальных элементов лагранжиана, где переменная является множителем ККТ, это совпадает с требованием выполнения ограничений простого числа:

    $ \displaystyle \frac{\partial L}{\partial \alpha_j} = 1 – y_j (\langle w, x_j \rangle + b) \leq 0$

    Далее, теорема ККТ говорит, что нужно иметь обе возможности двойственности:

    $ \displaystyle \alpha_j \geq 0 \text{ для всех } j$

    И, наконец, дополнительные условия нежесткости,

    $ \displaystyle \alpha_j (1 – y_j (\langle w, x_j \rangle + b)) = 0 \text{ для всех } j = 1, \dots, m$

    Для полной ясности: двойственная задача для SVM — это просто обобщенный лагранжиан: 9m y_j \alpha_j = 0$

    Все приведенные выше ограничения в виде равенства (нулевой лагранжиан, дополнительная нежесткость и это ограничение-напоминание) являются следствием теоремы ККТ.

    На данный момент мы готовы вывести и реализовать алгоритм последовательной минимальной оптимизации и запустить его на некоторых данных. Мы сделаем это в следующий раз.

    Нравится:

    Нравится Загрузка…

    Страница не найдена – Khoury College Development

     

    В мире, где информатика (CS) везде, CS для всех. CS пересекает все дисциплины и отрасли.

     

    Колледж компьютерных наук Хури стремится создавать и развивать разнообразную инклюзивную среду.

     

    Колледж Хури, первый в стране колледж информатики, основанный в 1982 году, вырос в размерах, разнообразии, программах на получение степени и превосходстве исследований.

     

    В наших региональных кампусах, расположенных в промышленных и технологических центрах, Колледж Хури предлагает сильные академические программы в оживленных городах для жизни, работы и учебы.

     

    Khoury College — это сообщество людей, преданных обучению, наставничеству, консультированию и поддержке студентов по всем программам.

     

    Программы награждения колледжей и университетов проливают свет на выдающихся преподавателей, студентов, выпускников и отраслевых партнеров.

     

    Наши реальные исследования, выдающиеся преподаватели, выдающиеся докладчики, динамичные выпускники и разные студенты рассказывают свои истории и попадают в новости.

     

    В Колледже Хури обучение происходит в классе и за его пределами. Мероприятия в нашей сети кампусов обогащают образовательный опыт.

     

    Информатика повсюду. Студенты Khoury College занимаются соответствующей работой, исследованиями, глобальными исследованиями и опытом обслуживания, которые помогают им расти.

     

    Магистранты углубляют свои знания посредством проектной работы, профессионального опыта работы и научного ассистента.

     

    Работа над исследованиями с преподавателями занимает центральное место в работе доктора философии. Докторанты колледжа Хури также могут проводить исследования с отраслевыми партнерами.

     

    Преподаватели и студенты Khoury College проводят эффективную работу по различным дисциплинам. Благодаря широкому спектру областей исследований мы каждый день решаем новые проблемы в области технологий.

     

    Наши институты и исследовательские центры объединяют ведущих академических, отраслевых и государственных партнеров для использования вычислительной мощности.

     

    Исследовательские проекты, разработанные и проводимые профессорско-преподавательским составом Khoury College мирового уровня, вовлекают студентов и других исследователей в получение новых знаний.

     

    Исследовательские лаборатории и группы сосредотачиваются на ряде проблем в определенном контексте, поощряя исследования и сотрудничество.

     

    Эта новая инициатива направлена ​​на устранение рисков для конфиденциальности и личных данных с помощью коллективных усилий на низовом уровне с упором на прозрачность и подотчетность.

     

    Современное оборудование, бесшовные системы и инновационные лаборатории и помещения позволяют нашим преподавателям и студентам проводить передовые исследования.

     

    9Колледж 0002 Khoury гордится нашим совместным инклюзивным сообществом. Каждый день мы стремимся создавать программы, которые приветствуют самых разных студентов в CS.

     

    Более 20 компьютерных клубов в колледже Хури и Северо-Восточном колледже предлагают что-то для каждого студента. Мы всегда рады новым членам на каждом уровне.

     

    Учащиеся учатся в современных классах, конференц-залах для совместной работы, а также в ультрасовременных лабораториях и исследовательских центрах.

     

    Сети обеспечивают безопасную и бесперебойную работу кода, современное и надежное оборудование, а наша квалифицированная системная команда управляет поддержкой и обновлениями.

     

    Заинтригован Колледжем Хури и северо-восточным университетом? Начните здесь, чтобы увидеть общую картину: академические науки, экспериментальное обучение, студенческая жизнь и многое другое.

     

    Готовы сделать следующий шаг в технической карьере? Наши магистерские программы сочетают в себе академическую строгость, исследовательское превосходство и значимые экспериментальные возможности.

     

    Добро пожаловать в магистерскую программу Align, предназначенную для людей, готовых добавить информатику (CS) в свой набор навыков или переключиться на совершенно новую карьеру в области технологий.

     

    Будучи аспирантом Хури, вы погрузитесь в строгую учебную программу, будете сотрудничать с известными преподавателями и окажете влияние на выбранную вами область исследований.

     

    Где бы вы ни находились на пути бакалавриата в Хури, у нас есть консультанты, ресурсы и возможности, которые помогут вам добиться успеха и сделать информатику доступной для всех.

     

    Где бы вы ни находились на пути к аспирантуре Хури, наши консультанты, информационные ресурсы и возможности помогут вам выбрать индивидуальный путь.

     

    В любой момент пути Align — и в любом из наших кампусов — консультанты Khoury, ресурсы и возможности поддержат вас на пути к карьере в сфере технологий.

     

    Консультанты и преподаватели помогут вам пройти путь докторантуры в Khoury College — от исследовательских пространств и междисциплинарных проектов до студенческой жизни и ресурсов.