Сзв м дополняющая форма: Дополняющая форма СЗВ-М: как заполнить, буде ли штраф

машин опорных векторов, двойная формулировка, квадратичное программирование и последовательная минимальная оптимизация | by Suraj Donthi

Это математически ориентированный подход к интуиции, лежащей в основе SVM, и алгоритмов оптимизации, используемых для ее решения. Эта статья служит универсальным руководством по демистификации внутренней работы SVM.

Машина опорных векторов (или первоначально автор — Владимир Вапник называл Сети опорных векторов) использует совершенно иной подход к решению статистических задач (в конкретной Классификации). Этот алгоритм активно использовался в нескольких задачах классификации, таких как классификация изображений, классификатор Bag-of-Words, OCR, прогнозирование рака и многие другие. SVM в основном представляет собой бинарный классификатор, хотя его можно модифицировать для многоклассовой классификации, а также для регрессии. В отличие от логистической регрессии и других моделей нейронных сетей, SVM пытаются максимизировать разделение между двумя классами точек. Блестящая идея использована автором.

Ниже приведены концепций, которые мы рассмотрим в этой статье , которые шаг за шагом демистифицируют SVM, а затем улучшают алгоритм, устраняя его недостатки.

  1. Ванильный (обычный) SVM и его целевая функция
  2. Мягкая маржа SVM
  3. Хитрость ядра
  4. Приложение 1. Вывод уравнения максимальной маржи. & Целевая функция
  5. Приложение 2. Поиск оптимума Целевой фн. с использованием лагранжиана, двойной формулировки и квадратичного программирования
    ∘ General method to solve for minima
    ∘ Solving for minima when constraints are present
    ∘ Kuhn — Tucker Conditions
    ∘ Duality & Complementary Slackness
  6. Appendix 3 — Deducing Optima for Soft Margin SVM
  7. Conclusion
  8. References

Let’s просто возьмите формальное определение SVM из Википедии:

Машина опорных векторов строит гиперплоскость или набор гиперплоскостей в многомерном или бесконечномерном пространстве, которые можно использовать для классификации, регрессии или других задач, таких как обнаружение выбросов. .

Подождите, слишком много технических терминов! Давайте просто упростим его и сохраним только необходимую информацию!

Во-первых, SVM создает гиперплоскость ( простая линия в n измерениях ). Как и в приведенном ниже GIF, эта гиперплоскость должна наилучшим образом разделить два класса пополам. Это все, что делают SVM… Остальное — начинка! ( бесконечномерное пространство, регрессия, обнаружение выбросов и т. д. )

Теперь построим ОПТИМАЛЬНАЯ ГИПЕРПЛОСКОСТЬ поддерживает две другие гиперплоскости, которые параллельны и равноудалены от нее с обеих сторон!

Эти две опорные гиперплоскости лежат в самых крайних точках между классами и называются опорными векторами .

Следовательно, нам просто нужно найти опорные гиперплоскости ( используя для простоты ), которые имеют максимальное расстояние между ними! Отсюда мы можем легко получить ОПТИМАЛЬНЫЙ ГИПЕРПЛАН . Это называется просто Гиперплоскость максимальной маржи .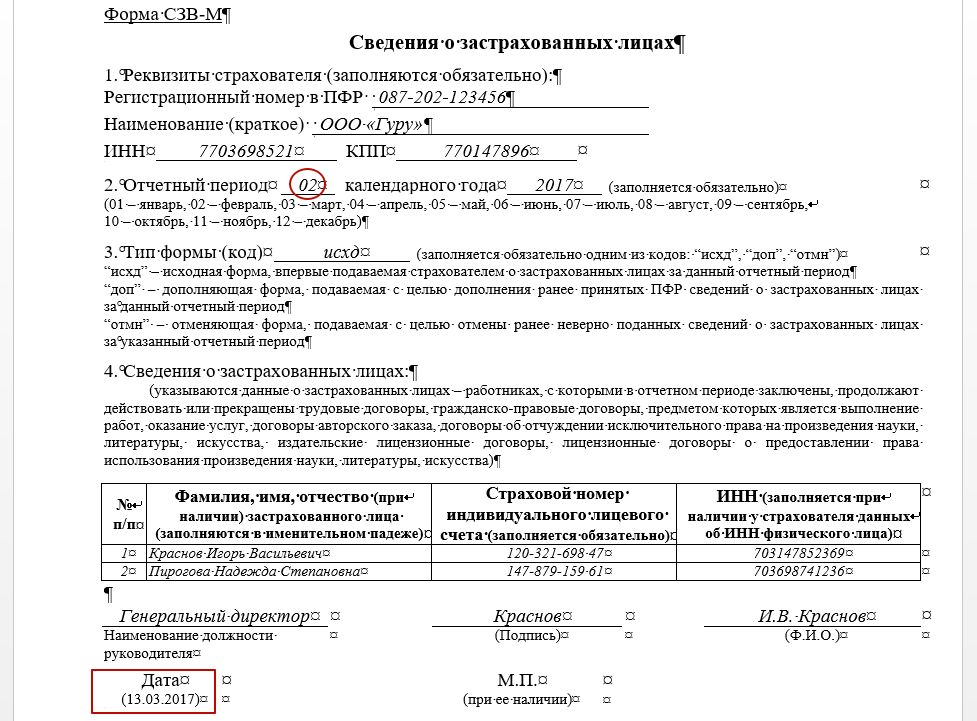 Расстояние между опорными гиперплоскостями называется Margin .

Источник: изображение автора

Следовательно, наша цель — просто найти максимальный запас M. Используя векторные операции, мы можем найти это (учитывая ОПТИМАЛЬНУЮ ГИПЕРПЛОСКОСТЬ ( w.x+b=0 ) ), Маржа равна:

Следовательно, Максимальная маржа M :

Для удобства математики Целевая функция принимает вид (подробное объяснение в Приложении 1):

Заметим, что наша цель сводилась к нахождению оптимального w из уравнения w.x+b= 0 !

Однако это также связано с ограничением, заключающимся в том, что точки в классе не должны лежать в пределах двух опорных гиперплоскостей! Математически это можно представить как:

Так что же означают эти ограничения?

Это означает, что внутри гиперплоскости не может быть точек, как показано на рисунке ниже, и это называется Hard Margin SVM (Vanilla SVM).

Источник: изображение автора

Это большой недостаток SVM! Два класса должны быть полностью разделимы. Этого никогда не бывает в реальных наборах данных! Вот где Soft Margin SVM вступают в игру🎉😃!

Прежде чем двигаться дальше, всего один вопрос! Используют ли SVM градиентный спуск для поиска минимумов ? Ни за что! (большинство людей этого не знают). Минимумы находятся непосредственно путем решения производных Objective функции . Поскольку существуют ограничения, нам нужно сначала взять лангранжиан целевой функции , чтобы найти минимумы. Вы можете найти полный вывод в Приложении 2 (рекомендую вам прочитать его!).

Как упоминалось выше, SVM Soft Margin могут обрабатывать классы с неотделимыми точками данных. Рисунок ниже ясно объясняет то же самое!

Итак, вот суть идеи Soft Margin:

Чтобы позволить SVM делать некоторые ошибки и при этом сохранить максимально широкое поле.

Источник: изображение автора

Теперь, как он может это сделать, но не ванильные SVM? Этот фактор представляет собой расстояние, которое точка данных превышает от соответствующей опорной гиперплоскости до другого класса.

Следовательно, если точка данных находится в пределах границы (опорной гиперплоскости), штрафной коэффициент 𝜉 ᵢ равно 0. В противном случае, если точка данных находится на другой стороне, этот коэффициент 𝜉 ᵢ равен его расстоянию между точкой данных и опорной гиперплоскостью. Следовательно, значение 𝜉 ᵢ является неотрицательным числом.

Это можно резюмировать следующим уравнением:

В идеале оно должно представлять количество « ошибок », которые делает SVM. Следовательно, наша новая целевая функция будет:

Здесь для малой степени 𝜎 функция F становится количеством ошибок! (Сумма используется для учета 𝜉 ᵢ всех точек в наборе данных)

Как и для SVM, минимумы могут быть найдены непосредственно путем решения ее производных (лагранжиана производных).

Теперь, оглядываясь назад на то, что мы получили, становится ясно, что мы используем только w.x+b . Это просто линейное уравнение. Это означает, что SVM работает лучше всего, когда вы можете классифицировать данные линейно!

Нелинейные данные. Источник: изображение автора

Это еще одно действительно огромное ограничение! Однако авторы нашли для этого лайфхак💃!! и это трюк с ядром. Проще говоря:

Ядро просто преобразует нелинейные точки данных в линейные точки данных, так что SVM может разделить два класса пополам.

То же самое показано на рисунке ниже.

Преобразование из n-измерения в N-измерение. Источник: Wikimedia

Следовательно, новое уравнение линии будет

Здесь используется хитрый прием для преобразования точек n-измерения в N-измерение , где N>n .

Ядро 𝜑 должно соответствовать следующим условиям:

Источник: изображение автора

Для SVM используется несколько функций ядра. Вот некоторые из популярных:

  • Гауссова радиальная базисная функция (RBF) :

, где 𝛾 > 0 .

Особый случай: 𝛾 = 1/2𝜎²

  • Gaussian Kernel :
  • Polynomial Kernel :
  • Sigmoid kernel :

For deriving the Objective function, we assume that the dataset is linearly separable.

Мы знаем, что две опорные гиперплоскости лежат на опорных векторах и между ними нет точек. Следовательно, мы можем сначала рассмотреть срединную гиперплоскость между этими двумя опорными гиперплоскостями:

И учитывая, что расстояние между этой и опорной гиперплоскостями равно 1, мы получаем

Поскольку нет точек, превышающих эти две гиперплоскости, мы можем сделать вывод, что:

Для всех значений с меткой yᵢ=+1

& для всех значений с меткой yᵢ=-1 ,

Мы можем комбинировать два, как показано ниже:

Следовательно, это ограничение для нашей целевой функции (см. то же самое в начале статья).

Теперь, чтобы найти максимальную маржу, ее нужно представить в виде гиперплоскостей. Итак, давайте выведем связь между Margin M и гиперплоскостями.

Источник: Изображение от автора

На приведенной выше рисунке пусть векторы X₀ и Z ₀ Be Parallel Vector на строках W.x+B = -1 w.x+b=1 соответственно. Затем

где вектор k является линией, перпендикулярной вектору x₀ и z ₀ .

величина вектора K IS M.

Следовательно,

Сейчас с Z ₀ и X₀ Lie Lie On и x₀ Lie On и x₀ Lie On и x₀ Lie on и x₀ Lie on и . 1 и w.x+b=-1 ,

Из приведенного выше уравнения. заменив z ₀ ,

Теперь, когда у нас есть, нам нужно максимизировать его,

Следовательно, новая цель, т.е. Целевая функция:

и ограничение неравенства:

Общий метод решения для минимумов

Чтобы найти оптимумы для кривой, мы можем просто

  1. Взять производную первого порядка,
  2. Приравнять производную к 0 (для максимумов или минимумов), чтобы получить дифференциальное уравнение.
  3. Решите дифференциальное уравнение, чтобы найти оптимальные точки.
  4. Производная 2-го порядка может указать направление, и, следовательно, мы можем сделать вывод, является ли оптимум минимумом или максимумом.

Нахождение минимумов при наличии ограничений

Если в дифференциальном уравнении есть некоторые ограничения, подобные тому, что мы имеем в нашей Целевой функции, нам сначала нужно применить множители Лагранжа (что, честно говоря, довольно прямолинейно) !

Если вы наблюдаете приведенное выше уравнение (5), это просто Целевая функция, вычтенная ограничением неравенства! Он должен удовлетворять только критериям αᵢ > 0 , когда ограничение является ограничением равенства. Однако приведенные выше уравнения представляют собой уравнения ограничения неравенства . Таким образом, дополнительный набор условий, называемый условиями Куна — Таккера, также должен удовлетворяться. Мы пройдемся по условиям позже.

Для нахождения оптимумов, как и прежде, возьмем производную первого порядка и приравняем ее к 0:

Чтобы найти оптимальные значения, мы можем просто подставить значения обратно в (5),

Расширяя уравнение. (5) мы получаем,

Теперь подставляя значения в (6) и (7) выше,

Мы можем повторно подставить значение w в уравнение. (6) к приведенному выше уравнению,

Здесь W называется Целевой функционал и является функцией всех ( αᵢ … to … αₙ

0)0053 представлен как Λ (Capital Lambda).

Этот вывод был необходим для учета ограничения неравенства [уравнение. (4)]. Поскольку теперь это учтено, целевой функционал W является новой функцией, которую необходимо оптимизировать вместо уравнения. (3). Это называется ДВОЙНОЙ ФОРМУЛИРОВКОЙ , потому что исходная Целевая функция была изменена!

В то время как Экв. (3) был свернут, W должен быть максимизирован.

Поскольку W является квадратным уравнением, это задача квадратичного программирования (QP), и ее можно решить с помощью алгоритма, называемого Sequential Minimal Optimization (SMO) . Если вы когда-либо пользовались пакетом LibSVM, который является базой для SVM в Scikit-Learn и большинстве других библиотек SVM, вы обнаружите, что пакет LibSVM реализует алгоритм SMO для расчета максимальной маржи !

Наконец, переходим к условиям, которым должны удовлетворять ограничения неравенства.

Kuhn — Условия Tucker

  1. Двойная осуществимость :

2. Бесплатная осуществимость :

3. Стационарные условия :

4. Primal Feasebibite (New & Complementary Slackness

Когда проблема может быть преобразована в другую задачу, решение которой легче вычислить, а также обеспечивает решение исходной задачи, говорят, что две проблемы демонстрируют Двойственность и наоборот.

Однако все двойные функции не обязательно должны иметь решение, обеспечивающее оптимальное значение для другой. Это можно сделать из приведенного ниже Рис. 1 , где существует Разрыв Двойственности между первичной и двойной проблемой. В рис. 2 двойственные задачи демонстрируют сильную двойственность и, как говорят, имеют дополнительную нежесткость . Кроме того, из приведенного ниже графика видно, что задача минимизации преобразуется в задачу максимизации. Следовательно, нам нужно максимизировать W против αᵢ .

Источник: изображение автора

Как описано ранее, целевая функция для SVM Soft Margin:

Здесь функция F — монотонная выпуклая функция, а C — константа регуляризации.

Следовательно, лагранжиан приведенной выше Целевой функции равен

Используя ту же методологию, что и в методе Hard Margin SVM, мы получаем Целевой функционал as,

Если вы заметили, лишний член здесь,

Где,

И ограничения для Целевого функционала:

Следовательно, решая Целевой функционал, мы можем получить оптимальную максимальную маржу.

Из приведенных выше разделов мы можем сделать вывод, что

  1. Базовые SVM или SVM с жесткой маржой представляют собой бинарные и линейные классификаторы, которые работают только с разделяемыми данными.
  2. SVM Soft Margin могут работать с неразделимыми данными.
  3. Ядра можно использовать для преобразования нелинейных данных в линейные данные, к которым можно применять SVM для двоичной классификации.
  4. Комбинация SVM может использоваться для выполнения многоклассовой классификации.
  5. Машины опорных векторов — это чрезвычайно быстрые алгоритмы, поскольку они напрямую определяют максимальную маржу и не используют итеративный процесс, такой как градиентный спуск, для поиска минимумов.
  1. Бумага о сетях опорных векторов.
  2. https://www.svm-tutorial.com/2014/11/svm-understanding-math-part-1/
  3. https://www.svm-tutorial.com/2014/11/svm-understanding- математика-часть-2/
  4. https://www.svm-tutorial.com/2015/06/svm-understanding-math-part-3/
  5. https://www.svm-tutorial.com/2016/09/unconstrained-minimization/
  6. https://www.svm-tutorial.com/2016/09/convex-functions/
  7. https://www.svm-tutorial.com/2016/09/duality-lagrange-multipliers/
  8. Опорный вектор Machines Succinctly by Alexandre Kowalczyk
  9. Ali Ghodsi, Lec 12: Машина опорных векторов с мягкими границами (SVM)
  10. https://www.ncbi. nlm.nih.gov/pmc/articles/PMC5822181/
  11. https://www.youtube.com/watch?v=JTTiELgMyuM

11. http://fourier.eng.hmc.edu/e161/lectures/svm/

12. http://www. svcl.ucsd.edu/courses/ece271B-F09/handouts/SoftSVMs.pdf

13. Лекция 70 — SVM с мягкой маржей | Добыча массивных наборов данных | Стэнфордский университет

Базовая реализация SVM с мягким запасом на ядре в Python — Эндрю Таллох

26 ноября 2013 г.

Машины опорных векторов (SVM) — это семейство хороших контролируемых методов обучения.
алгоритмы, которые могут обучать модели классификации и регрессии
эффективно и с очень хорошей производительностью на практике.

SVM также основаны на выпуклой оптимизации и теории гильбертова пространства.
и есть много красивой математики в выводе
различные аспекты алгоритма обучения, которые мы рассмотрим в
последующие посты.

Сейчас мы просто дадим введение в основную теорию
SVM ядра с мягкой маржой. Классическое лечение начинается с
линейные SVM с жесткими маржами, затем познакомьтесь с трюком ядра и
формулировка с мягкой маржой, так что это несколько быстрее, чем другие
презентации. 9d$ — функция такая, что матрица $K$ с $K_{ij} =
\kappa(x_i, x_j)$ является положительно полуопределенной. Ключевое свойство таких
функций ядра состоит в том, что существует карта $\nu$ такая, что $\langle
\nu(x), \nu(y) \rangle = \kappa(x, y)$. Можно думать о $\nu$ как
отображение наших входных функций в выходное пространство более высокого измерения.

Мы можем показать, что для заданного отображения признаков $\nu$, удовлетворяющего
предыдущее условие, лагранжиан для задачи нахождения
гиперплоскость с максимальным запасом принимает вид: 9Т з
\end{уравнение}
при условии $z\geq 0$ и $\langle z, y \rangle = 0$.

По результирующему вектору множителей Лагранжа $z$ находим, что
большинство $z$ равны нулю. Это происходит от комплементарной небрежности
условия в нашей задаче оптимизации — либо $(x_i, y_i)$ находится на
максимальная маржа (и поэтому соответствующий множитель Лагранжа отличен от нуля),
или это не предел (и поэтому множитель Лагранжа равен нулю).

Предсказание заданного вектора признаков $x$ принимает форму
\начать{выравнивать}
\метка{уравнение:1}
\langle w, \nu(x) \rangle &= \sum_{i=1}^{n} z_{i} y_{i} \langle \nu(x_{i}),
\nu(x) \rangle \
&= \sum_{i=1}^{n} z_{i} y_{i} \каппа(x_{i}, x)
\end{align} где мы можем взять сумму только по ненулевым $z_{i}$.

Это дает очень эффективный алгоритм предсказания — как только мы получим
обучила нашу SVM, большое количество обучающих данных (эти образцы
с нулевыми множителями Лагранжа) можно удалить.

Есть больше сложностей (обработка термина смещения, обработка
неразделимые наборы данных), но в этом суть алгоритма.

Реализация

Полная реализация обучения (с использованием cvxopt в качестве
квадратичный программный решатель) на Python приведен ниже:

Код не требует пояснений и следует данному обучению.
алгоритм довольно точно. Чтобы вычислить наши множители Лагранжа, мы
просто постройте матрицу Грама и решите данную QP. Затем мы проходим
наши обученные опорные векторы и соответствующие им лагранжевые векторы
множители и веса для SVMPredictor , реализация которого
приведен ниже.

Это просто реализует приведенное выше уравнение прогнозирования.

Примерный список функций ядра приведен в

Демонстрация

Демонстрируем рисование пар независимых стандартных нормальных переменных
как функции и пометить $y_i = sign(\sum x)$.