Срок сдачи сзв м за июнь 2018: образец заполнения, сроки сдачи, штраф

Срок сдачи отчета СЗВ-М в 2018 году

СЗВ-М – это ежемесячный отчет, который компании и ИП начали сдавать с 1 апреля 2016 года. В 2018 году срок сдачи отчета – не позднее 15 числа месяца, следующего за отчетным. Но что делать, если последний день выпал на выходной или праздничный день?

На основании письма Пенсионного фонда РФ от 28.12.2016 г. № 08-19/19045, страхователь ежемесячно не позднее 15-го числа месяца, следующего за отчетным периодом – месяцем, представляет сведения о каждом работающем у него застрахованном лице. Отчетность представляется по форме СЗВ-М, утвержденной постановлением Правления ПФР от 01.02.2016 № 83п.

Вместе с тем Законом № 27-ФЗ не определен порядок переноса представления отчетности, если последний день срока приходится на выходной и (или) нерабочий праздничный день.

Одновременно следует отметить, что в случаях, когда отношения прямо не урегулированы законодательством, к таким отношениям, если это не противоречит их существу, применяется законодательство, регулирующее сходные отношения (аналогия закона).

В соответствии со статьей 193 Гражданского кодекса Российской Федерации, если последний день срока приходится на нерабочий день, днем окончания срока считается ближайший следующий за ним рабочий.

Таблица сроков сдачи СЗВ-М в 2018 году















Отчетный месяц 2018 года

Последний день сдачи отчета СЗВ-М

Декабрь 2017 года

15 января 2018 года

Январь 2018 года

15 февраля 2018 года

Февраль 2018 года

15 марта 2018 года

Март 2018 года

16 апреля 2018 года

Апрель 2018 года

15 мая 2018 года

Май 2018 года

15 июня 2018 года

Июнь 2018 года

16 июля 2018 года

Июль 2018 года

15 августа 2018 года

Август 2018 года

17сентября 2018

Сентябрь 2018 года

15 октября 2018 года

Октябрь 2018 года

15 ноября 2018 года

Ноябрь 2018 года

17 декабря 2018 года

Декабрь 2018 года

15января 2019 года

При заполнении отчета СЗВ-М следует внимательно заполнять код месяца, за который вы отчитываетесь, чтобы потом не было споров с Пенсионным Фондом. В поле «Отчетный период» СЗВ-М надо указать правильный код месяца, за который вы подаете отчет. Посмотрите нашу таблицу, пожалуйста:






Код

Месяц

Код

Месяц

Код

Месяц

01

Январь

05

Май

09

Сентябрь

02

Февраль

06

Июнь

10

Октябрь

03

Март

07

Июль

11

Ноябрь

04

Апрель

08

Август

12

Декабрь

Год, за который отчитываетесь, укажите в поле «Календарный год». Например, при подаче в 2018 году отчета за январь 2018 года в этом поле поставьте «2018».

Способ сдачи отчета СЗВ-М в 2018 году

Отчет СЗВ-М можно сдавать следующими способами:

1) Можно сдать на бумажном носителе вручную при личном посещении Управления ПФР в вашем городе,

2) Можно отправить документ по почте ценным письмом с описью вложения,

3) Можно сдать электронно. Но стоит помнить, что при численности сотрудников более 25 человек сдавать отчет следует только в электронном виде.

Срок сдачи СЗВ-М не зависит от способа представления отчета в ПФР.

Разместить:

Silvercorp Metals Inc (SVM) Дивиденды

Сводка дивидендов

Ожидается, что следующие дивиденды Silvercorp Metals Inc превысят через 15 дней и будут выплачены через 1 месяц .

Предыдущий дивиденд Silvercorp Metals Inc составлял 1,25 цента, и он ушел от 5 месяцев назад и был выплачен 5 месяцев назад .

Обычно выплачивается 2 дивиденда в год (исключая специальные акции), а покрытие дивидендов составляет примерно 2,0.

Последние дивиденды

Сводка Предыдущий дивиденд Следующий дивиденд
Статус Платный Прогноз
Тип Финал Промежуточный
За акцию 1,615с (1,25с) Требуется регистрация
Дата декларации 27 мая 2022 г. (пт) 07 ноя 2022 (пн)
Дата выпуска 03 июня 2022 г. (пт) 22 ноября 2022 г. (вт)
Дата выплаты 24 июня 2022 г. (пт) 14 декабря 2022 г. (ср)

Введите количество
Сильверкорп Металс Инк
акции, которыми вы владеете, и мы рассчитаем ваши дивидендные выплаты:

Предыдущий платеж

1,62 канадских доллара (1,25 доллара США)

Оплачено 24 июня 2022 г.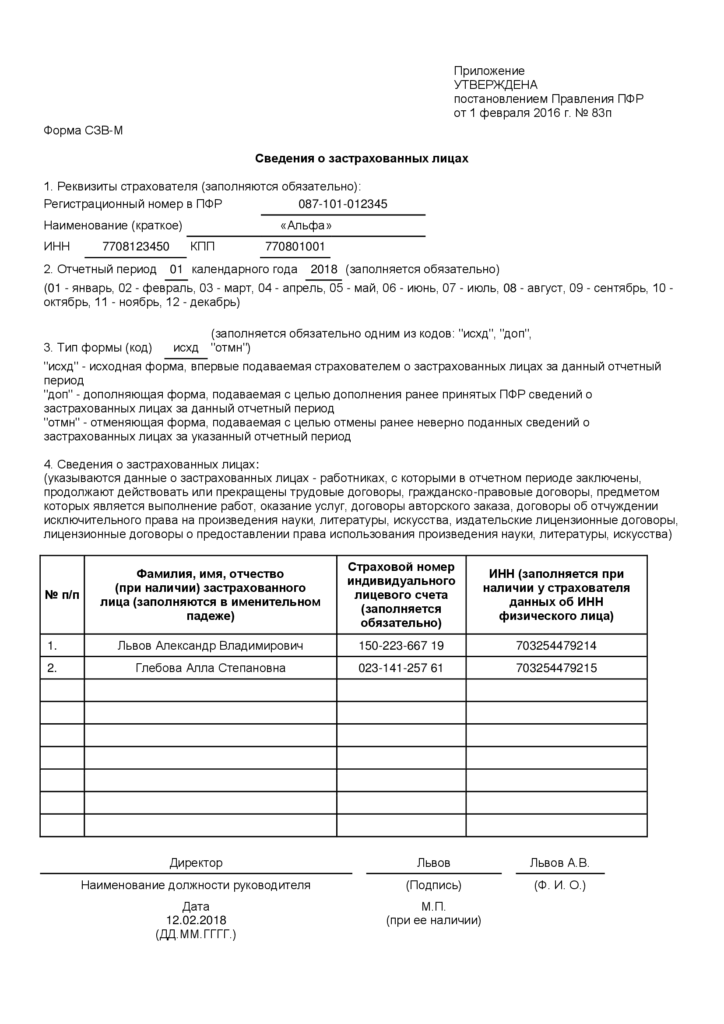 (пт)

Следующий платеж

Требуется регистрация

Выплачено 14 декабря 2022 г. (ср)

Точность прогноза

100%

Наши инструменты премиум-класса предсказали Silvercorp Metals Inc со 100% точностью.

Пробная премия

Дивидендный доход сегодня

0,9%

Дивидендный доход рассчитывается путем деления годовой выплаты дивидендов на действующую цену акции

В таблице ниже показана полная история дивидендов Silvercorp Metals Inc. Прогноз Финал 23 мая 2025 г. 30 мая 2025 г. 27 июня 2025 г.

долларов США

Зарегистрироваться — Прогноз Промежуточный 04 ноя 2024 19 ноя 2024 11 декабря 2024

долларов США

Зарегистрироваться — Прогноз Финал 24 мая 2024 г. 31 мая 2024 года 28 июня 2024 г.

долларов США

Зарегистрироваться — Прогноз Промежуточный 06 ноя 2023 21 ноя 2023 13 декабря 2023 г.

долларов США

Зарегистрироваться — Прогноз Финал 26 мая 2023 г. 02 июня 2023 г. 30 июня 2023 г.

долларов США

Зарегистрироваться — Прогноз Промежуточный 07 ноя 2022 22 ноя 2022 14 декабря 2022 г.

долларов США

Зарегистрироваться — Платный Финал 27 мая 2022 г. 03 июня 2022 г. 24 июня 2022 г.

долларов США

1.25c 1.25c 😄 Платный Промежуточный 08 ноя 2021 23 ноя 2021 15 декабря 2021 г.

долларов США

1.25с 1.25c 😄 Платный Финал 26 мая 2021 г. 03 июн 2021 25 июня 2021 г.

долларов США

— 1.25c Платный Промежуточный 10 ноя 2020 24 ноя 2020 16 дек. 2020

долларов США

— 1.25c Платный Финал 28 мая 2020 г. 04 июн 2020 26 июня 2020 г.

долларов США

— 1.25c Платный Промежуточный 12 ноя 2019 26 ноя 2019 18 декабря 2019 г.

долларов США

— 1.25c Платный Финал – 06 июн 2019 28 июня 2019 г.

долларов США

— 1. 25c Платный Промежуточный 15 ноября 2018 г. 27 ноя 2018 19 декабря 2018 г.

долларов США

— 1.25c Платный Финал 28 мая 2018 г. 07 июня 2018 г. 29 июня 2018 г.

долларов США

— 1.25c Платный Промежуточный 09 ноя 2017 27 ноября 2017 г. 19 декабря 2017 г.

долларов США

— 1с Платный Финал 26 мая 2017 г. 07 июн 2017 30 июня 2017 г.

долларов США

— 1с Платный Промежуточный 04 ноя 2016 24 ноября 2016 г. 19 декабря 2016 г. CAD — 1с Платный Ежеквартально – 26 июня 2015 г. 21 июля 2015 г. CAD — 0,5с Платный Ежеквартально 13 февраля 2015 г. 27 марта 2015 г. 21 апреля 2015 г. CAD — 0,5с Платный Ежеквартально 14 ноября 2014 г. 29 декабря 2014 г. 21 января 2015 г. CAD — 0,5с Платный Ежеквартально 15 августа 2014 г. 26 сентября 2014 г. 21 октября 2014 г. CAD — 0,5с Платный Ежеквартально 23 мая 2014 г. 26 июня 2014 г. 18 июля 2014 г.

долларов США

— 0,46с Платный Ежеквартально 14 февраля 2014 г. 27 марта 2014 г. 21 апреля 2014 г.

долларов США

— 0,44с Платный Ежеквартально 15 ноября 2013 г. 27 декабря 2013 г. 21 января 2014 г.

долларов США

— 2.35c Платный Ежеквартально 08 авг. 2013 26 сентября 2013 г. 21 октября 2013 г.

долларов США

— 2.43с Оплачено Ежеквартально 22 мая 2013 г. 26 июня 2013 г. 19 июля 2013 г.

долларов США

— 2.37с Платный Ежеквартально 14 февраля 2013 г. 26 марта 2013 г. 22 апреля 2013 г.

долларов США

— 2.44с Платный Ежеквартально 13 ноября 2012 г. 27 декабря 2012 г. 21 января 2013 г.

долларов США

— 2.51с Платный Ежеквартально – 26 сентября 2012 г. 21 октября 2012 г.

долларов США

— 2.55c Платный Ежеквартально – 27 июня 2012 г. 20 июля 2012 г.

долларов США

— 2.43с Платный Ежеквартально – 28 марта 2012 г. 21 апреля 2012 г.

долларов США

— 2.52с Платный Ежеквартально – 28 декабря 2011 г. 20 января 2012 г.

долларов США

— 2.45c
2006 0. 0с —
2007 0.0с

0%

2008 0.0с

0%

2009 0.0с

0%

2010 0.0с

0%

2011 0.0с

0%

2012 7.5c

100%

2013 10.0с

33,3%

2014 5.5c

-45,0%

2015 2.0c

-63,6%

2016 0,5с

-75,0%

2017 2.302598с

360,5%

2018 2.944342с

27,9%

2019 3.317413с

12,7%

2020 3. 345517с

0,8%

2021 3.132444с

-6,4%

2022 Требуется регистрация
2023 Требуется регистрация
2024 Требуется регистрация
2025 Требуется регистрация

Оптимизированная диаграмма дивидендов Silvercorp Metals Inc.

На приведенной ниже диаграмме показаны оптимизированные дивиденды по этой ценной бумаге за скользящий 12-месячный период.

Дивидендный доход сегодня
0,9%
Оптимизированный выход
Требуется регистрация
Максимум за 52 недели
1,6%
на
26 сентября 2022 г.
52-недельный минимум
0,6%
на
23 ноября 2021 г.
Обратный отсчет даты следующего бывшего отдела
Требуется регистрация

О компании Silvercorp Metals Inc.

Silvercorp Metals Inc. (Silvercorp) — горнодобывающая компания, производящая металлы серебра, свинца и цинка в концентратах на рудниках в Китае. Компания вместе со своими дочерними предприятиями занимается приобретением, разведкой, разработкой и добычей полезных ископаемых. Silvercorp управляет несколькими серебряно-свинцово-цинковыми рудниками, в том числе Ying Mining District в провинции Хэнань, Китай, серебряно-свинцово-цинковым рудником Gaocheng (GC) в провинции Гуандун, Китай, и золото-свинцово-цинковым рудником BYP в провинции Хунань. Горнодобывающий район Ин состоит из нескольких рудников, включая SGX, HPG, TLP, LME, LMW и HZG. Район SGX включает небольшое спутниковое месторождение. Его рудник HPG представляет собой серебряно-золото-свинцовый комплекс, расположенный в центральной части района Ин. TLP — это свинцово-серебряный рудник, расположенный примерно в 11 км к востоку-юго-востоку от SGX. Шахта GC занимает площадь 5,5 квадратных километров (км2), которая расположена примерно в 200 километрах (км) к западу от города Гуанчжоу. Его рудник BYP имеет разрешение на добычу площадью около 3,67 км2.

Сектор
Горное дело
Страна
Канада
Цена акции
3,58 канадских доллара
(вчерашняя цена закрытия)
Акции выпуска
177 миллионов
Рыночная капитализация
634 млн канадских долларов
Покрытие дивидендов

Во сколько раз дивиденды покрываются доходом компании. Покрытие 1 означает, что весь доход выплачивается в виде дивидендов

2,0
КАДИ

Последовательное ежегодное увеличение дивидендов — количество лет, в течение которых компания увеличивает свои дивиденды

1
Рыночные индексы
нет

Статьи не найдены

Идентификация вибрации при фрезеровании зеркал с использованием Q-фактора и SVM

  • «>

    Liu HB, Wang YQ, Jia ZY, Guo DM (2015) Стратегия интеграции машинных измерений (OMM) и числового программного управления (NC) обработка крупногабаритных тонкостенных деталей с коррелятивной зависимостью поверхности. Int J Adv Manuf Technol 80 (9–12):1721–1731

    Артикул

    Google ученый

  • Lan J, Lin B, Huang T, Xiao JL, Zhang XF, Fei JX (2017) Планирование траектории для опорных головок в системе зеркально-фрезерной обработки. Int J Adv Manuf Technol 91(1):617–628

    Статья

    Google ученый

  • Фанг Б., Девор Р.Е., Капур С.Г. (2001) Упруго-динамическая модель фрикционного контакта и ее влияние на динамику системы заготовка-крепление. J Manuf Sci Eng 123 (3): 481–489

    Артикул

    Google ученый

  • Коллуру К., Аксинте Д. (2013) Парное взаимодействие динамических реакций инструмента и заготовки при тонкостенном фрезеровании. J Mater Process Technol 213(9):1565–1574

    Статья

    Google ученый

  • Quintana G, Ciurana J (2011) Вибрация в процессах обработки: обзор. Int J Mach Tools Manuf 51(5):363–376

    Артикул

    Google ученый

  • Лю Т., Ян С., Чжан В. (2016) Частотно-временной анализ сигналов нестационарной вибрации для развертываемых конструкций с использованием нестационарного преобразования Габора с постоянной добротностью. Mech Syst Signal Process 75:228–244

    Статья

    Google ученый

  • Cao H, Zhou K, Chen X (2015) Идентификация вибрации в процессе торцевого фрезерования на основе EEMD и нелинейных безразмерных индикаторов. Int J Mach Tools Manuf 92: 52–59

    Артикул

    Google ученый

  • Бин Г. Ф., Гао Дж. Дж., Ли С. Дж., Диллон Б. С. (2012) Ранняя диагностика неисправностей вращающихся машин на основе вейвлет-пакетов — извлечение признаков декомпозиции эмпирических мод и нейронная сеть. Mech Syst Signal Process 27:696–711

    Статья

    Google ученый

  • Пэн З.К., Чу Ф.Л. (2004) Применение вейвлет-преобразования в мониторинге состояния машин и диагностике неисправностей: обзор с библиографией. Процесс обработки сигналов механической системы 18 (2): 199–221

    Артикул

    Google ученый

  • Liu C, Zhu L, Ni C (2017) Идентификация вибрации при концевом фрезеровании на основе комбинации EMD и WPD. Int J Adv Manuf Technol 91(9):3339–3348

    Статья

    Google ученый

  • Shao H, Shi X, Li L (2011) Разделение сигналов мощности в процессе фрезерования на основе вейвлет-преобразования и анализа независимых компонентов. Int J Mach Tools Manuf 51 (9):701–710

    Артикул

    Google ученый

  • Hu CZ, Yang Q, Huang MY, Yan WJ (2017) Разделение слепых источников на основе анализа разреженных компонентов с недоопределенным определением для выделения признаков неисправности подшипника в редукторе ветряной турбины. Iet Renew Power Gener 11(3):330–337

    Статья

    Google ученый

  • Чжун З.М., Чен Дж., Чжун П., Ву Дж.Б. (2006) Применение метода слепого разделения источников для выделения звуковых сигналов машин. Int J Adv Manuf Technol 28 (9):855–862

    Артикул

    Google ученый

  • Plaza EG, López PJN (2017) Мониторинг шероховатости поверхности с помощью анализа сингулярного спектра сигналов вибрации. Mech Syst Signal Process 84:516–530

    Статья

    Google ученый

  • «>

    Zhang Z, Li H, Meng G, Tu X, Cheng C (2016) Обнаружение вибрации в процессе фрезерования на основе энергетической энтропии VMD и WPD. Int J Mach Tools Manuf 108: 106–112

    Артикул

    Google ученый

  • Huang P, Li J, Sun J, Zhou J (2012) Анализ вибрации при фрезеровании титанового сплава на основе обработки сигналов силы резания. Int J Adv Manuf Technol 64 (5–8): 613–621

    Google ученый

  • Liu Y, Wang X, Lin J, Zhao W (2015) Раннее обнаружение вибрации в процессе шлифования зубчатых колес с использованием тока двигателя сервопривода. Int J Adv Manuf Technol 83 (9–12):1801–1810

    Google ученый

  • Дрон Дж.П., Боларс Ф., Расолофондрайбель (2004) Улучшение чувствительности скалярных индикаторов (крест-фактор, эксцесс) с использованием метода шумоподавления путем спектрального вычитания: применение для обнаружения дефектов в шарикоподшипниках. J Sound Vib 270(1–2):61–73

    Артикул

    Google ученый

  • Аль-Гамд А.М., Мба Д. (2006) Сравнительное экспериментальное исследование по использованию акустической эмиссии и анализа вибрации для выявления дефектов подшипника и оценки размера дефекта. Процесс обработки сигналов Mech Syst 20(7):1537–1571

    Артикул

    Google ученый

  • Fu Y, Zhang Y, Zhou H, Li D, Liu H, Qiao H, Wang XQ (2016) Своевременное онлайн-обнаружение вибрации в процессе торцевого фрезерования. Mech Syst Signal Process 75:668–688

    Статья

    Google ученый

  • Wang YQ, Bo QL, Liu HB, Lian M, Wang F, Zhang J (2017) Декомпозиция полных колебательных компонентов из шумных сигналов механической вибрации путем минимизации колебаний добротности. Trans Inst Meas Control 39(9):1313–1328

    Артикул

    Google ученый

  • «>

    Sims ND (2005) Коэффициент демпфирования самовозбуждения: критерий вибрации для моделирования фрезерования во временной области. J Manuf Sci Eng 127(3):433–445

    Статья

    Google ученый

  • Cai G, Chen X, He Z (2013) Разложение сигнала с использованием разреженности с использованием настраиваемого вейвлет-преобразования Q-фактора для выделения признаков неисправности коробки передач. Процесс обработки сигналов механической системы 41 (1–2): 34–53

    Артикул

    Google ученый

  • Selesnick IW (2011) Разреженные представления сигналов с использованием настраиваемого вейвлет-преобразования добротности. Труды SPIE — the. Int Soc Opt Eng 8138(3):815–822

    Google ученый

  • Wang WQ, Golnaraghi MF, Ismail F (2004) Прогноз состояния работоспособности машин с использованием нейро-нечетких систем.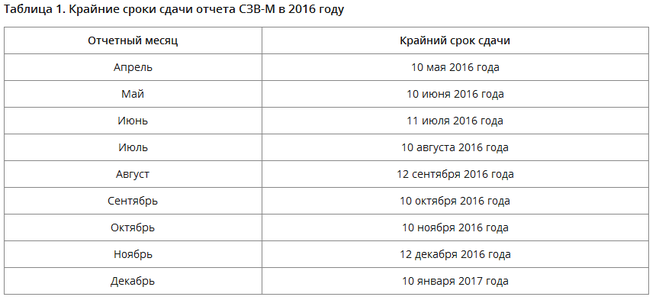 Процесс обработки сигналов Mech Syst 18(4):813–831

    Артикул

    Google ученый

  • Нешат М., Адели А., Сепиднам Г., Сарголзаи М. (2012) Предсказание состава бетонной смеси с использованием адаптивных нейронно-нечетких систем вывода и систем нечеткого вывода. Int J Adv Manuf Technol 63(1):373–390

    Статья

    Google ученый

  • Peng Y, Dong M (2011) Метод прогнозирования с использованием возрастной скрытой полумарковской модели для прогнозирования состояния оборудования. Процесс обработки сигналов Mech Syst 25(1):237–252

    Артикул

    Google ученый

  • Kong D, Chen Y, Li N (2017) Метод скрытой полумарковской модели для оценки износа инструмента в процессе фрезерования. Int J Adv Manuf Technol 92(9):3647–3657

    Статья

    Google ученый

  • «>

    Yang Y, Yu D, Cheng J (2007) Подход к диагностике неисправностей роликового подшипника на основе спектра огибающей IMF и SVM. Измерение 40(9–10):943–950

    Артикул

    Google ученый

  • Тан Ф., Инь М., Ван Л., Инь Г. (2018) Устойчивое моделирование тепловой ошибки шпинделя с использованием LASSO и LS-SVM. Int J Adv Manuf Technol 94(5):2861–2874

    Статья

    Google ученый

  • Бхат Н.Н., Датта С., Вашист Т., Пал С., Пал С.К., Сен Р. (2016) Мониторинг состояния инструмента с помощью SVM-классификации изображений обработанных поверхностей при токарной обработке. Int J Adv Manuf Technol 83 (9):1487–1502

    Артикул

    Google ученый

  • Yao Z, Mei D, Chen Z (2010) Обнаружение и идентификация вибраций в режиме онлайн на основе вейвлета и метода опорных векторов. J Mater Process Technol 210(5):713–719

    Статья

    Google ученый

  • Полито Ф., Петри А., Понтуале Г., Далтон Ф. (2010) Анализ акустической эмиссии при резке металла с помощью моделей временных рядов. Int J Adv Manuf Technol 48 (9):897–903

    Артикул

    Google ученый

  • Агдам Б.Х., Вахдати М., Садеги М.Х. (2015) Оценка износа основной задней поверхности инструмента на основе вибрации в процессе токарной обработки с использованием моделей ARMA. Int J Adv Manuf Technol 76(9):1631–1642

    Статья

    Google ученый

  • Мосаллам А., Меджахер К., Зерхуни Н. (2013) Моделирование непараметрических временных рядов для промышленной прогностики и управления здравоохранением. Int J Adv Manuf Technol 69(5):1685–1699

    Артикул

    Google ученый

  • «>

    Hoell S, Omenzetter P (2016) Оптимальный выбор коэффициентов авторегрессионной модели для раннего обнаружения повреждений применительно к лопастям ветряных турбин. Mech Syst Signal Process 70-71:557–577

    Статья

    Google ученый

  • Huang W, Sun H, Wang W (2017)Разложение разреженного сигнала на основе резонанса и его применение в диагностике механических неисправностей: обзор. Датчики 17(6)

  • Кортес С., Вапник В. (1995) Сети опорных векторов. Mach Learn 20(3):273–297

    МАТЕМАТИКА

    Google ученый

  • Смола А.Дж., Шёлькопф Б. (2004) Учебное пособие по регрессии опорных векторов. Stat Comput 14(3):199–222

    Статья
    MathSciNet

    Google ученый

  • Гриллиас К.С., Антониадис И.А. (2012) Метод опорных векторов, основанный на обучении физической модели для обнаружения неисправностей подшипников качения в промышленных условиях.