Содержание
Новая форма ЕФС-1 вместо СЗВ-ТД. СЗВ-СТАЖ, СЗВ-М. 4-ФСС и ДСВ-3: правила заполнения
Текст: Елена Карсетская – юрист, эксперт по трудовому праву. Автор многочисленных публикаций в профессиональных изданиях. Автор книг «Трудовые книжки», «Сокращение штата», «Прием и увольнение работников»; «Локальные акты организации» и других.
С 1 января 2023 года произойдет объединение Пенсионного фонда РФ и Фонда социального страхования РФ. Как следствие, изменятся формы и состав отчетности, которая будет представляться в объединенный фонд. Рассмотрим, что будет представлять собой новая форма ЕФС-1, которая заменит СЗВ-ТД. СЗВ-СТАЖ. СЗВ-М. 4-ФСС к ДСВ-3.
Изменения 2023 года: Социальный фонд России вместо ПФР и ФСС РФ
С 2023 года вместо Пенсионного фонда РФ и Фонда социального страхования РФ будет действовать единый фонд – Фонд пенсионного и социального страхования Российской Федерации (Федеральный закон от 14.07.2022 № 236-ФЗ «О Фонде пенсионною и социального страхования Российской Федерации»). Кратко фонд будет именоваться Социальный фонд России, а сокращенно – СФР.
Кратко фонд будет именоваться Социальный фонд России, а сокращенно – СФР.
Соответственно, с нового года станут неактуальными действующие сейчас формы. СЗВ-ТД. СЗВ-СТАЖ. СЗВ-М, 4-ФСС, ДСВ-3. Вместо данных форм будет введена единая форма сведений (п. 2 ст. 8 Федерального закона от 01.04.1996 № 27-ФЗ «Об индивидуальном (персонифицированном) учете в системах обязательного пенсионного страхования и обязательного социального страхования» в редакции, действующей с 01.03.2022). В единую форму войдет также информация о страховых взносах на обязательное социальное страхование (несчастные случай и профзаболевания), поэтому отпадает необходимость в отдельной форме 4-ФСС.
Новая форма ЕФС-1
На данный момент единая форма еще не утверждена, но Правление ПФР подготовило проект Постановления об утверждении единой формы и правилах ее заполнения. С максимальной долей вероятности, с 2023 года будет использоваться единая форма, предложенная данным проектом. Поэтому заранее ознакомимся с особенностями данного документа.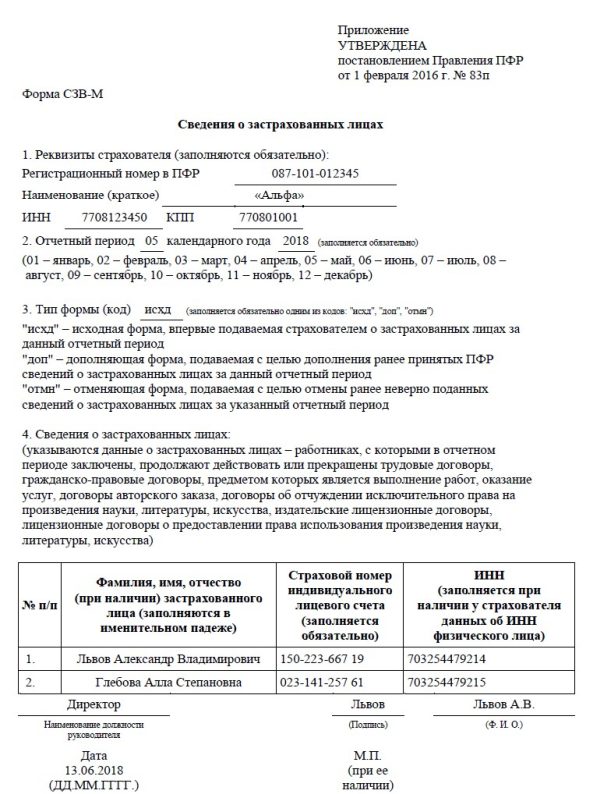
Итак, форма будет иметь краткое наименование ЕФС-1. Состоять она будет из титульного листа и двух разделов:
Раздел 1 – «Сведения о трудовой (иной) деятельности, страховом стаже, заработной плате и дополнительных страховых взносах на накопительную пенсию»;
Раздел 2 – «Сведения о начисленных страховых взносах на обязательное социальное страхование от несчастных случаев на производстве и профессиональных заболеваний».
Каждый раздел содержит еще несколько подразделов, которые имеют свои особенности заполнения и сроки представления. Нет необходимости всегда представлять полностью заполненную форму. Организация может представлять конкретные разделы и подразделы в соответствии с установленными сроками их представления (п. 1.11 Проекта, но титульный лист надо заполнять всегда, независимо от комплектации отчета).
Заполнение раздела 1
Раздел 1 фактически заменяет формы СЗВ-ТД, СЗВ-СТАЖ и ДСВ-3. Обратите внимание: в данный раздел надо будет включать информацию не только о работниках, но и об исполнителях по гражданско-правовым договорам.
Раздел 1 состоит из подразделов:
– подраздел 1 «Сведения о трудовой (иной) деятельности, страховом стаже, заработной плате зарегистрированного лица (ЗЛ)».
Этот подраздел содержит общие сведения о работнике (исполнителе по договору ГПХ). Поэтому заполнять этот подраздел надо обязательно, если вы заполняете один из следующих подразделов раздела 1.
– подраздел 1.1. «Сведения о трудовой (иной) деятельности»
Этот подраздел содержит информацию, которая сейчас отражается в СЗВ-ТД. Но еще раз отметим, что заполнять данный раздел надо будет не только, когда будут иметь место кадровые мероприятия в отношении работников, но и в отношении исполнителей по договорам ГПХ, поэтому появляются свои нюансы.
Вводятся новые коды «НАЧАЛО ДОГОВОРА ГПХ», «ОКОНЧАНИЕ ДОГОВОРА ГПХ». Отметим, что проект ЕФС-1 создавался до введения изменений в трудовое законодательство относительно необходимости приостановления трудовых договоров с мобилизованными работниками. Поэтому, очевидно, что Проект будет дополнен кодами «ПРИОСТАНОВЛЕНИЕ» и «ВОЗОБНОВЛЕНИЕ».
Представлять сведения из подраздела 1.1. надо будет по правилам, действующим сейчас в отношении формы СЗВ-ТД: при приеме/увольнении, заключении/расторжении договора ГПХ – не позднее следующего рабочего дня; при переводе, переходе на электронную трудовую книжку и пр. – не позднее 25-го числа следующего месяца.
– подраздел 1.2. «Сведения о страховом стаже»
Данный подраздел заменит форму СЗВ-СТАЖ. Состав информации во многом схож с действующей формой, но имеются нюансы. Например, вводится графа «Занятость» в разделе «Условия досрочного назначения страховой пенсии», а также информация о результатах СОУТ. Сдавать подраздел надо не позднее 25 января следующего года.
– подраздел 1.3 – актуален только для работников государственных и муниципальных учреждений.
– подраздел 2 – заполняется в случае, если работники имеют право на досрочную пенсию. Сдавать подраздел надо не позднее 25 января следующего года.
– подраздел 3 – «Сведения о застрахованных лицах, за которых перечислены дополнительные страховые взносы на накопительную пенсию и уплачены взноси работодателя». Повторяет сведения, которые сейчас отражаются в ДСВ-3.
Повторяет сведения, которые сейчас отражаются в ДСВ-3.
Сдавать подраздел надо ежеквартально, не позднее 25-го числа месяца, следующего за отчетным кварталом.
Заполнение раздела 2
Раздел 2 формы ЕФС-1 в принципе повторяет действующую сейчас форму 4-ФСС. Сдавать раздел надо ежеквартально, не позднее 25 числа месяца, следующего за отчетным кварталом.
Отчётность в ПФР, ФСС и другие госорганы удобно подготовить, отредактировать и отправить через сервис электронной отчётности компании Такском «Онлайн-Спринтер».
Преимущества «Онлайн-Спринтера»
1. Веб-решение
Минимальные требования к рабочему месту – мощный компьютер необязателен.
2. Всегда актуальные версии форм отчётности
Вовремя обновляются вслед за изменениями законодательства.
3. Сверка с бюджетом и с контрагентами
Сверяйтесь с ФНС и ПФР – бесплатно во всех тарифах, причём с ФНС – в автоматическом режиме. Сверяйте книги покупок и продаж – бесплатно во всех тарифах.
4. Удобная работа с несколькими компаниями
Сдавайте отчётность за несколько организаций в одном интерфейсе.
5. Поддержка клиентов 24/7
Телефон и e-mail – круглосуточно.
Чат – на сайте, в интерфейсе программы, в личном кабинете – с 9:30 до 18:00 (мск), по будням.
Интересует электронная отчетность?
Имя
Просьба заполнить имя, чтобы консультант знал как к вам обращаться
Номер телефона
Заполните поле телефон, чтобы консультант вам перезвонил
Я согласен на обработку персональных данных
Нажимая на кнопку, я выражаю свое согласие с обработкой персональных данных ООО «Такском»
отчетность ФСС ПФР онлайн-отчетность ФПСС СФР
Отправить
Запинить
Твитнуть
Поделиться
Обзор SVM, двойственности Лагранжа и условий ККТ
Эта статья является частью моего обзора курса машинного обучения. Он знакомит с классификатором машины опорных векторов ( SVM ), формой соответствующей выпуклой оптимизации и тем, как использовать Двойственность Лагранжа и Условия ККТ для решения задачи оптимизации. Кроме того, в нем также рассказывается, как использовать приемы ядра для выполнения нелинейной классификации.
Кроме того, в нем также рассказывается, как использовать приемы ядра для выполнения нелинейной классификации.
Некоторые изображения в этой статье взяты из слайдов курса доктора Джойс Хо.
Обзор метода опорных векторов (SVM)
Рассмотрим задачу классификации линейно-разделимого случая.
SVM-1
Поскольку существует более одной границы для полного разделения этих двух классов, какое из них является лучшим решением?
По сути, SVM решает, что лучшим разделителем строк (или гиперплоскостей в больших размерах) является тот, у которого максимальный запас (как показано ниже). В идеале каждый образец должен выходить за пределы поля. Чем больше поле, тем больше мы уверены, что невидимый образец будет правильно классифицирован. SVM работает довольно хорошо как в теории, так и на практике.
SVM-2
Понятие разделителя и поля легко увидеть для линейно-разделимого случая. Что, если есть такие шумы, что никакая гиперплоскость не может полностью разделить два класса? Или, что еще хуже, что, если два класса вообще не являются линейно разделимыми (например, граница — гиперсфера)?
Краткие ответы:
- Упомянутая выше концепция называется «жесткая маржа».
 Но на самом деле данные обычно не полностью линейно-разделимы. Обобщая, SVM допускает некоторую слабину вокруг разделителя, что означает, что он допускает некоторые неправильно классифицированные выборки с гиперпараметром, который указывает силу штрафа $C$. Чем больше сила штрафа, тем меньше ошибочно классифицированных образцов, но также и меньше разница (а это не то, что нам нужно). Большое значение $C$ приведет к переоснащению, а значение $C$ представляет собой компромисс между скоростью ошибочной классификации и простотой модели. Маржа с провисанием называется «мягкой маржой». В этой статье для простоты мы рассмотрим только «жесткую» оптимизацию.
Но на самом деле данные обычно не полностью линейно-разделимы. Обобщая, SVM допускает некоторую слабину вокруг разделителя, что означает, что он допускает некоторые неправильно классифицированные выборки с гиперпараметром, который указывает силу штрафа $C$. Чем больше сила штрафа, тем меньше ошибочно классифицированных образцов, но также и меньше разница (а это не то, что нам нужно). Большое значение $C$ приведет к переоснащению, а значение $C$ представляет собой компромисс между скоростью ошибочной классификации и простотой модели. Маржа с провисанием называется «мягкой маржой». В этой статье для простоты мы рассмотрим только «жесткую» оптимизацию. - Для нелинейного граничного случая SVM использует «уловки ядра» для вычисления многомерных признаков. Трюк с ядром — это способ эффективного вычисления внутреннего произведения двух многомерных векторов без обращения к высоким размерностям. Позже в этой статье мы увидим, почему мы можем использовать ядра в SVM.
Таким образом, вот две ключевые идеи SVM:
- Установите разделитель с наибольшим запасом, чтобы сделать его надежным
- Используйте трюки ядра для эффективного вычисления большего пространства функций
Задача оптимизации (случай с жесткими границами)
Базовые компоненты (обзор знаний)
- Целевой разделитель для соответствия: $wx + b = 0$, который является гиперплоскостью.
 $w$ и $b$ — это параметры, которые SVM должен изучить на обучающих выборках. Обратите внимание, что $w$ — вектор нормали к этой гиперплоскости; $wx + b = 0$ означает, что все векторы, ортогональные вектору $w$ (с точкой пересечения $b$), образуют гиперплоскость.
$w$ и $b$ — это параметры, которые SVM должен изучить на обучающих выборках. Обратите внимание, что $w$ — вектор нормали к этой гиперплоскости; $wx + b = 0$ означает, что все векторы, ортогональные вектору $w$ (с точкой пересечения $b$), образуют гиперплоскость. - Расстояние от точки $x’$ до целевой гиперплоскости: $\dfrac{wx’ + b}{\Vert w\Vert}$.
- Доказательство: выберите любую точку $x$ на гиперплоскости. Расстояние от $x’$ до гиперплоскости равно проекции вектора $x’ – x$ на вектор нормали $w$. Следовательно, расстояние $ = \Vert x’ – x\Vert \cdot \cos (x’-x, w) \\=\Vert x’ – x\Vert \cdot \dfrac{w(x’-x)}{ \Vert w\Vert\Vert x’ – x\Vert} \\= \dfrac{wx’ – wx}{\Vert w\Vert} =\dfrac{wx’ + b}{\Vert w\Vert}$
- Предположим, что метки равны $+1, -1$. Запас $\gamma_i$, образованный образцом $x_i$: $\gamma_i = \dfrac{y_i(wx_i + b)}{\Vert w\Vert}$. При правильной классификации $\gamma_i > 0$.
SVM-3
Задача оптимизации
Цель состоит в том, чтобы максимизировать границу, когда все выборки имеют расстояние больше, чем граница (ни одна выборка не находится внутри области поля). Его можно представить следующей оптимизационной задачей:
Его можно представить следующей оптимизационной задачей:
$$
\max_{w, b} \quad \gamma\\
\text{s.t.} \quad \gamma_i \geq \gamma
$$
Умножим $ \Vert w\Vert$ на ограничениях, так что $\Vert w\Vert$ больше не является знаменателем.
$$
\max_{w, b} \quad \gamma\\
\text{s.t.} \quad y_i(wx_i + b) \geq \gamma \Vert w\Vert
$$
Пусть $\hat{\gamma} = \gamma \Vert w\Vert$. Поэтому $\gamma =\hat{\gamma} / \Vert w\Vert$.
$$
\max_{w, b} \quad \dfrac{\hat{\gamma}}{\Vert w\Vert}\\
\text{s.t.} \quad y_i(wx_i + b) \geq \ hat{\gamma}
$$
Обратите внимание, что в отличие от $\gamma$ значение $\hat{\gamma}$ на самом деле не имеет значения. Мы можем задать шкалу $\lambda$ для $w$ и $b$, которая масштабирует $\hat{\gamma}$ до $\lambda\hat{\gamma}$, и цель та же самая: $\dfrac{ \lambda \hat{\gamma}}{\lambda \Vert w\Vert} =\dfrac{\hat{\gamma}}{\Vert w\Vert}$. Поэтому разные значения $\hat{\gamma}$ не меняют оптимизацию. мы можем просто установить $\hat{\gamma} = 1$. Теперь проблема оптимизации: 92}{2}\\
мы можем просто установить $\hat{\gamma} = 1$. Теперь проблема оптимизации: 92}{2}\\
\text{s.t.} \quad y_i(wx_i + b) \geq 1
$$
Двойственность Лагранжа и условия ККТ
Давайте временно отложим оптимизацию SVM и рассмотрим общие подходы к решению оптимизационных задач с ограничениями.
Оптимизация с ограничениями-равенствами
Мы можем просто построить лагранжиан $\mathcal{L}(w, \beta)$ и установить частные производные $w$ и $\beta$ равными $0$, чтобы найти $w $ и $\бета$. Он выражается следующим образом.
Задача оптимизации:
$$
\min_w \quad f(w)\\
\text{s.t.} \quad h_i(w) = 0
$$
Лагранжиан:
$$
\mathcal{L }(w, \beta) = f(w) + \sum \beta_ih_i(w)
$$
Оптимизация с ограничениями-неравенствами
Мы называем задачу основной задачей оптимизации, и для ее решения мы сначала строим обобщенный лагранжиан.
Задача оптимизации:
$$
\min_w \quad f(w)\\
\begin{align}
\text{s.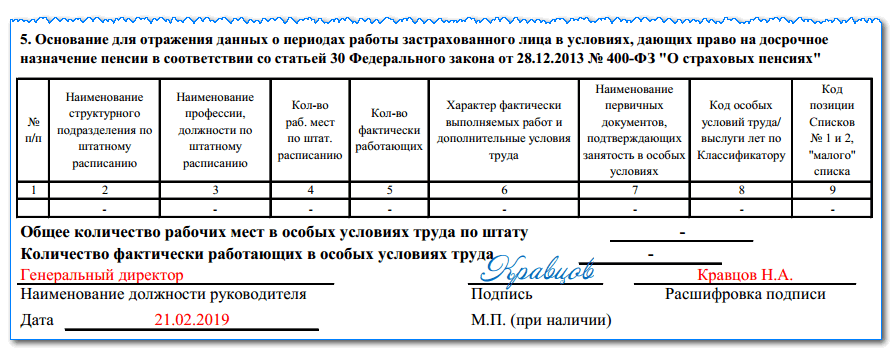 t.} \quad h_i(w) = 0\\
t.} \quad h_i(w) = 0\\
g_i(w) \leq 0
\end{align}
$$
Обобщенный лагранжиан:
$$
\mathcal {L}(w, \alpha, \beta) = f(w) + \sum \alpha_i g_i(w) + \sum \beta_i h_i(w)
$$
Теперь наша задача состоит в том, чтобы минимизировать $\mathcal{ L}(ш, \альфа, \бета)$. Перепишем основную задачу в другом виде. Рассмотрим следующую задачу, где $w$ может нарушать ограничения:
$$
\max_{\alpha, \beta: \alpha_i \geq 0} \mathcal{L}(w, \alpha, \beta)
$$
Обратите внимание, что если $w$ удовлетворяет всем ограничениям $g_i(w) \leq 0$ и $h_i(w) = 0$, то максимум лагранжиана равен $f(w)$, когда $\ альфа = 0$. Если $w$ нарушает любое i-е ограничение, максимум лагранжиана равен $+\infty$, потому что мы можем установить $\alpha_i$ или $\beta_i$ так, чтобы $\alpha_i g_i(w)$ или $\beta_i h_i (w)$ равно $+\infty$. Следовательно, $\max_{\alpha, \beta: \alpha_i \geq 0} \mathcal{L}(w, \alpha, \beta)$ принимает одно и то же значение исходной цели $f(w)$ для всех значений $w$, которые удовлетворяют ограничениям. Это может быть выражено как:
Это может быть выражено как:
$$
\max_{\alpha, \beta: \alpha_i \geq 0} \mathcal{L}(w, \alpha, \beta) =
\begin{case}
f(w) \quad w \ text{ удовлетворяет всем основным ограничениям}\\
+\infty \quad \text{Иначе}
\end{cases}
$$
Если мы затем добавим минимизацию, следующая новая задача оптимизации будет такой же, как исходная основная задача проблема.
$$
\min_w \max_{\alpha, \beta: \alpha_i \geq 0} \mathcal{L}(w, \alpha, \beta)
$$
Мы также можем взглянуть на его двойной проблема. Двойная проблема здесь состоит в том, чтобы просто изменить порядок «макс.» и «мин.»: 9*$. Следовательно, если задача оптимизации удовлетворяет всем условиям ККТ, мы можем либо решить прямую задачу напрямую (что часто бывает сложно), либо решить двойственную задачу (что встречается чаще).
$$
\begin{align}
\dfrac{\partial \mathcal{L}}{w_i} &= 0\\
\dfrac{\partial \mathcal{L}}{\beta_i} &= 0\ \
\alpha_i g_i(w) &= 0\\
g_i(w) &\leq 0\\
\alpha_i &\geq 0
\end{align}
$$
Соблюдая приведенные выше условия, мы можем видеть первые два условия совпадают с условиями Лагранжа. 2}{2} – \sum \alpha_i [y_i (wx_i + b) – 1]
2}{2} – \sum \alpha_i [y_i (wx_i + b) – 1]
$$
Из условий ККТ мы знаем, что когда $y_i (wx_i + b) – 1 < 0$, $\alpha_i = 0$; и $\alpha_i$ будет ненулевым только тогда, когда $y_i (wx_i + b) – 1 = 0$. Такие выборки $(x_i, y_i)$ называются опорными векторами и лежат на целевом поле. Размер опорных векторов намного меньше размера обучающей выборки. На рисунке ниже те три образца, которые лежат на краю, являются опорными векторами.
SVM-2
Первичная и двойственная задача 92}{2} – \sum \alpha_i [y_i (wx_i + b) – 1]
$$
Другой способ представить максимальное число
Чтобы решить двойственную задачу, нам нужно сначала минимизировать лагранжиан относительно $ w$ и $b$. Следовательно, возьмем частную производную от $w$ и $b$ и приравняем к ней $0$, получим два других уравнения:
Частная производная от $w$ до $0$:
$$
\begin{align}
\dfrac {\ partial \ mathcal {L}} {w} &= 0 \\
w — \sum \alpha_i y_i x_i &= 0\\
w &= \sum \alpha_i y_i x_i
\end{align}
$$
Частная производная от $b$ до $0$:
$$
\begin{align}
\dfrac{\partial \mathcal{L}}{b} &= 0\ \
\sum \alpha_i y_i &= 0
\end{align}
$$
Подставим эти два уравнения в лагранжиан, получим:
$$
\mathcal{L}(w, b, \alpha) = \sum \alpha_i – \dfrac{1}{2} \sum_{i, j} y_i y_j \alpha_i \alpha_j x_i x_j
$$
Следующая задача состоит в решении следующей оптимизации.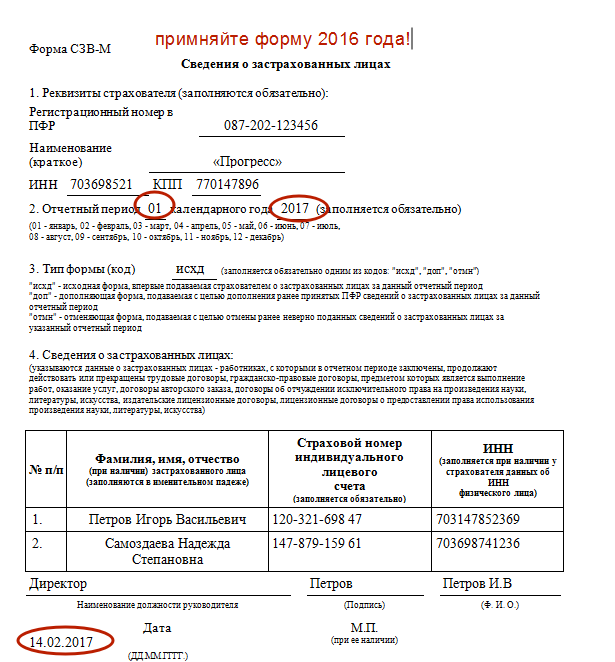 Мы называем это двойной версией SVM: 9* y_i
Мы называем это двойной версией SVM: 9* y_i
Кроме того, для предсказания единственная операция над входом $x$ — это вычисление скалярного произведения между $x$ и опорными векторами: $
Ядро имеет следующий вид:
$$K(x, z) = \Phi(x) \cdot \Phi(z)$$
, где $\Phi$ — отображение пространственных признаков. Ядро $K(x, z)$ вычисляет скалярное произведение двух пространственных отображений путем прямого сопоставления внутреннего произведения двух входных векторов, что часто дешевле по сравнению с $\Phi(x) \cdot \Phi(z) $.
Одним из популярных ядер является полиномиальное ядро, и мы можем использовать его для увеличения степени пространства функций в SVM.
Метод опорных векторов с отображением признаков Дирихле
. 2018 февраль;98:87-101.
doi: 10.1016/j.neunet.2017.11.006.
Epub 2017 16 ноября.
Али Недайе
1
, Амир Аббас Наджафи
2
Принадлежности
- 1 Факультет промышленной инженерии, К.Н. Технологический университет Туси, Тегеран, Иран.
- 2 Факультет промышленной инженерии, К.Н. Технологический университет Туси, Тегеран, Иран.
 Электронный адрес: [email protected].
Электронный адрес: [email protected].
PMID:
29223012
DOI:
10.1016/j.neunet.2017.11.006
Али Недайе и др.
Нейронная сеть.
2018 9 фев.0011
. 2018 февраль;98:87-101.
doi: 10.1016/j.neunet.2017.11.006.
Epub 2017 16 ноября.
Авторы
Али Недайе
1
, Амир Аббас Наджафи
2
Принадлежности
- 1 Факультет промышленной инженерии, К.
 Н. Технологический университет Туси, Тегеран, Иран.
Н. Технологический университет Туси, Тегеран, Иран. - 2 Факультет промышленной инженерии, К.Н. Технологический университет Туси, Тегеран, Иран. Электронный адрес: [email protected].
PMID:
29223012
DOI:
10.1016/j.neunet.2017.11.006
Абстрактный
Машина опорных векторов (SVM) — это алгоритм обучения с учителем для анализа данных и распознавания закономерностей. Стандартный SVM имеет некоторые ограничения в задачах нелинейной классификации. Чтобы преодолеть эти ограничения, нелинейная форма SVM представляет собой модифицированную машину, основанную на функциях ядра или других нелинейных отображениях функций, устраняющих упомянутое несовершенство. Однако выбор эффективного ядра или функции сопоставления признаков сильно зависит от структуры данных. Таким образом, гибкое отображение признаков можно с уверенностью применять к разным типам структур данных, не усложняя выбор ядра и его настройку. В этой статье представлен новый гибкий подход к отображению признаков, основанный на распределении Дирихле, с целью разработки эффективной SVM для нелинейных структур данных. Для определения параметров отображения Дирихле используется метод настройки, основанный на оценке максимального правдоподобия и методе оптимизации Ньютона. Численные результаты иллюстрируют превосходство предложенной машины по показателям точности и относительной частоты ошибок по сравнению с традиционными.
Однако выбор эффективного ядра или функции сопоставления признаков сильно зависит от структуры данных. Таким образом, гибкое отображение признаков можно с уверенностью применять к разным типам структур данных, не усложняя выбор ядра и его настройку. В этой статье представлен новый гибкий подход к отображению признаков, основанный на распределении Дирихле, с целью разработки эффективной SVM для нелинейных структур данных. Для определения параметров отображения Дирихле используется метод настройки, основанный на оценке максимального правдоподобия и методе оптимизации Ньютона. Численные результаты иллюстрируют превосходство предложенной машины по показателям точности и относительной частоты ошибок по сравнению с традиционными.
Ключевые слова:
распределение Дирихле; функция ядра; Нелинейное отображение; контролируемое обучение; Машина опорных векторов.
Copyright © 2017 Elsevier Ltd. Все права защищены.
Похожие статьи
Быстрая машина экстремального обучения с уменьшенным ядром.
Дэн В.Ю., Онг Ю.С., Чжэн К.Х.
Дэн В.Ю. и др.
Нейронная сеть. 2016 апр;76:29-38. doi: 10.1016/j.neunet.2015.10.006. Epub 2016 6 января.
Нейронная сеть. 2016.PMID: 26829605
Построение машинного классификатора опорных векторов с использованием алгоритма светлячка.
Чао С.Ф., Хорнг М.Х.
Чао С.Ф. и соавт.
Компьютер Intel Neurosci. 2015;2015:212719. дои: 10.1155/2015/212719. Epub 2015 23 февраля.
Компьютер Intel Neurosci. 2015.PMID: 25802511
Бесплатная статья ЧВК.Вицинальный классификатор опорных векторов с использованием контролируемой кластеризации на основе ядра.

Ян Х, Цао А, Сун Кью, Шефер Г, Су Ю.
Ян X и др.
Артиф Интелл Мед. 2014 март; 60(3):189-96. doi: 10.1016/j.artmed.2014.01.003. Epub 2014 7 февраля.
Артиф Интелл Мед. 2014.PMID: 24637294
Применение метода опорных векторов (SVM) для изучения геномики рака.
Хуанг С., Цай Н., Пачеко П.П., Наррандес С., Ван Ю., Сюй В.
Хуанг С. и др.
Протеомика геномики рака. 2018 янв-февраль;15(1):41-51. doi: 10.21873/cgp.20063.
Протеомика геномики рака. 2018.PMID: 29275361
Бесплатная статья ЧВК.Обзор.
Преодолеть переобучение диагностики опорных векторов.
Хан Х., Цзян Х.
Хан Х и др.
Рак Информ. 2014 9 декабря; 13 (Приложение 1): 145-58. DOI: 10.4137/CIN.S13875. Электронная коллекция 2014.
Рак Информ. 2014.PMID: 25574125
Бесплатная статья ЧВК.Обзор.
Посмотреть все похожие статьи
Цитируется
Общий молекулярный механизм и паттерны иммунной инфильтрации аневризм грудной и брюшной аорты.
He B, Zhan Y, Cai C, Yu D, Wei Q, Quan L, Huang D, Liu Y, Li Z, Liu L, Pan X.
Он Б. и соавт.
Фронт Иммунол. 2022 21 окт;13:1030976. doi: 10.3389/fimmu.2022.1030976. Электронная коллекция 2022.
Фронт Иммунол. 2022.PMID: 36341412
Бесплатная статья ЧВК.Подходы искусственного интеллекта и машинного обучения в структуре и открытии на основе лигандов лекарств, влияющих на центральную нервную систему.
Гаутам В., Гаурав А., Масанд Н., Ли В.С.
 , Патил В.М.
, Патил В.М.
Гаутам В. и др.
Мол Дайверс. 11 июля 2022 г. doi: 10.1007/s11030-022-10489-3. Онлайн перед печатью.
Мол Дайверс. 2022.PMID: 35819579
Обзор.
Диагностическая классификация рака по метилированию ДНК парараковых тканей.
Ма Б., Чай Б., Донг Х., Ци Дж., Ван П., Сюн Т., Гонг И., Ли Д., Лю С., Сонг Ф.
Ма Б и др.
Научный представитель 2022 23 июня; 12 (1): 10646. doi: 10.1038/s41598-022-14786-7.
Научный представитель 2022.PMID: 35739223
Бесплатная статья ЧВК.Подход машинного обучения к разработке прогностической подписи на основе транскриптомного профилирования помутнений матового стекла для точной классификации и изучения иммунной микросреды LUAD на ранней стадии.
Чжао З.


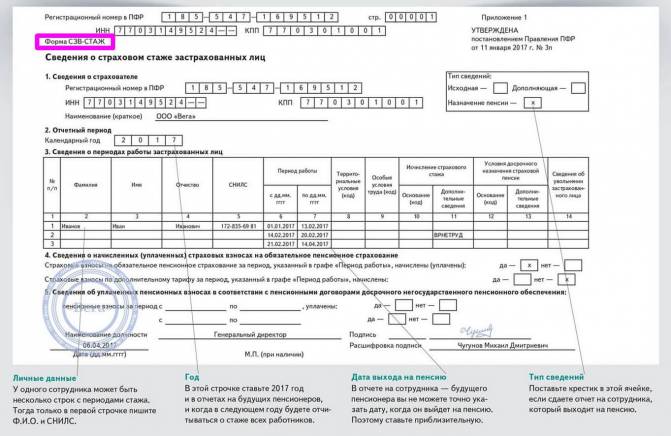 Но на самом деле данные обычно не полностью линейно-разделимы. Обобщая, SVM допускает некоторую слабину вокруг разделителя, что означает, что он допускает некоторые неправильно классифицированные выборки с гиперпараметром, который указывает силу штрафа $C$. Чем больше сила штрафа, тем меньше ошибочно классифицированных образцов, но также и меньше разница (а это не то, что нам нужно). Большое значение $C$ приведет к переоснащению, а значение $C$ представляет собой компромисс между скоростью ошибочной классификации и простотой модели. Маржа с провисанием называется «мягкой маржой». В этой статье для простоты мы рассмотрим только «жесткую» оптимизацию.
Но на самом деле данные обычно не полностью линейно-разделимы. Обобщая, SVM допускает некоторую слабину вокруг разделителя, что означает, что он допускает некоторые неправильно классифицированные выборки с гиперпараметром, который указывает силу штрафа $C$. Чем больше сила штрафа, тем меньше ошибочно классифицированных образцов, но также и меньше разница (а это не то, что нам нужно). Большое значение $C$ приведет к переоснащению, а значение $C$ представляет собой компромисс между скоростью ошибочной классификации и простотой модели. Маржа с провисанием называется «мягкой маржой». В этой статье для простоты мы рассмотрим только «жесткую» оптимизацию. $w$ и $b$ — это параметры, которые SVM должен изучить на обучающих выборках. Обратите внимание, что $w$ — вектор нормали к этой гиперплоскости; $wx + b = 0$ означает, что все векторы, ортогональные вектору $w$ (с точкой пересечения $b$), образуют гиперплоскость.
$w$ и $b$ — это параметры, которые SVM должен изучить на обучающих выборках. Обратите внимание, что $w$ — вектор нормали к этой гиперплоскости; $wx + b = 0$ означает, что все векторы, ортогональные вектору $w$ (с точкой пересечения $b$), образуют гиперплоскость.

 , Патил В.М.
, Патил В.М.